coe501

First 1-4 weeks of semester: Students are expected to independently carry out literature Survey on their selected topics, compile information of relevant papers in a progress report PR-1, have an action plan on their project implementation, and prepare for a presentation. During this period, the student is expected to carry out literature survey of no less than 4 technical papers on his project topic, interact with the instructor regarding the major issues of his project, and present the literature survey and planned implementation for the next phase. A 15-minute presentation is to be given in week 5 of the semester in front of the class students and course instructor. This part will be rated 25% of project for both presentation and timely submission of PR-1.
From week 5 to week 10, Students are expected to carry out the implementation part of their project by taking into account: (1) his presented or revised action plan, and (2) the instructor observations formulated during or after his presentation. During this period, the student is expected to interact with the instructor regarding the major design issues, difficulties in addressing some parts, resource problems, or any kind of problem that require specific attention to avoid negative impact on the project. Prepare report PR-2 after adding the implementation aspects presented above to P-1. A 15-minute presentation involving success and failure design and implementation aspects is to be given in week 11 in front of the class and instructor. This part will be rated 35% of project for both presentation and timely submission of PR-2.
From week 11 to week 14, Students are expected to carry out: (1) debugging and testing of their implementation and refer to instructor in case of problems, (2) carry out performance evaluation of the project with data collection, (3) revise PR-1 by including the performance evaluation and detailed analysis of collected results, (4) prepare the final project presentation. During this period, the student is expected to interact with the instructor regarding the debugging issues and performance interpretation. A presentation involving overall project will be delivered by the team (or student) before the last day of classes (week 15). The emphasis should be here on the method and results. This part will be rated 40% of project for both presentation and timely submission of PR-3 which is the final report. Here the student is to submit a zipped folder including all of original word reports (not pdf), well documented source code, evaluation data, and reference papers. A demo to the instructor will also be required.

The literature survey should focus on following topics: (1) review of dynamic execution micro-architectures (DEMA), (2) resolution of hazards in DEMA, and (3) methods of code restructuring for increasing ILP. The students will prepare presentations as stated in the Course Projects Working Framework. Investigation of the DLX simulator with respect to (1) take a code like ADI code, write it in C, generate its code in DLX, and collect its run time, (2) restructure the DLX ADI assembly to the best you can, run it, and compare its performance to the compiled version, (3) Try loop unrolling and compare performance. The above operation can be repeated for other code like the Ocean Red-Black, Solving a system of linear equations using Jacobi, etc. Based on the above experience, the student may advice a method for compiler loop restructuring such as the use of loop unrolling. Explain the compiler approach with respect to a source code in DLX and give example.

1. Consider a set (say 5) of small programs (computation loops) like the (1) Alternating Direction Integration (ADI), (2) the Red-Black Relaxation loop, (3) 2D Matrix Multiply, (4) Ocean Red-Black, and (5) Solving a system of linear equations using Jacobi.

2. Carry out recurrence analysis of each loop and classify it as LID, B-LCD, and F-LCD.

3. Restructure the loop to minimize its execution time using the loop unrolling and software pipelining.

4. Run each of the above programs without restructuring, with loop unrolling (possibly different configurations), and software pipelining (possibly different configurations) and collect performance data form the simulator.

5. Report performance at all levels after collecting the execution time as the number of clocks. Compare performance for each restructuring approach, and present your discussion and justification.

6. Suggest formal restructuring rules for loop unrolling and software pipelining.

7. Write a the program for a tool that takes a loop with a few statement in the body as input and (1) carry out data dependence analysis, (2) check the profitability of loop unrolling and software pipelining under specific dependence conditions, (3) restructure the loop using unrolling and / or software pipelining, (4) run the resulting loops on DLX and show the results.

For the first four weeks the students carry out (1) Surveying of I-pipelining techniques in at two recent micro-architectures, (2) review of dynamic execution models, (3) methods of resolving hazards, and (4) compiler techniques to improving ILP. The suggested plan is: (1) Surveying of I-pipelining techniques in recently proposed micro-architectures (last ten years), (2) how structural, data, and control hazards are resolved and at what level, (3) main proposed features like branch-prediction, speculation, etc., (4) provide a comparison of these micro-architectures with respect to major aspects especially expected performance and limitations. Implement a branch-prediction table with 2-bit history and evaluate performance by using typical loop structures. The students will prepare for a presentation within four weeks.

1. Select one branch prediction algorithm from a recent research paper and implement it. Carry out performance evaluation by using a statistically generated branch behavior. For example, the probability of some instruction to be a CB is 0.2 and that the branch has a Set of statistical T/NT patterns (for example pattern 1110010101 prob. taken is 0.6). Evaluate performance of the used branch prediction and suggest some improvement.

2. Select one correlating branch prediction algorithm from a recent research paper and implement it. Carry out performance evaluation by using a statistically generated branch behavior. For example, set up a a set of correlation rules between 3 or more CBs that are hidden to the computer. Each correlation element indicate the T/NT of each of the CBs. You may randomly a given element at a start of first CB. The problem is to evaluate the performance of the algorithm when the set correlated branches behaves as above. Study performance (correct prediction as compared incorrect ones) and suggest some algorithm tuning.

· Carry out literature survey using papers from the IEEE digital library and the Internet. Papers from this folder are old and should be avoided as main reference papers.

· The previous student papers Folder including the student report with his presentation and the two reference papers references. This means that the current students grades will depend on on the improvement, surplus work, and innovation they provide as compared to the provided student references and code.

· The student is recommended to implement a correlating branch predictor to improve the performance as compared to the previously implemented scheme (see item above).

· Task-1: carefully read (1) the class presentation, (2) the book, and (3) New references papers as well as those used by the previous student (see Folder above). Literature survey should be done basically on new papers.

· Task-2: Analyze the provided student implementation (code, presentation, and report): generation of branching cases, test program, collecting results. The student work is expected to noticeably improve the technical level of the current student approach and implementation. It is also expected that the student will implement the various schemes that will be presented in the lecture. The student work and grade will be based on improvement, surplus work, and innovative ideas presented as compared to the provided student work, implementation, and results.

7- Some additional course projects can be offered with the following titles: Performance Evaluation of a few Dynamic Brach Prediction Methods, Design of a Speculative Dynamic Execution Unit and performance evaluation, etc.

In Chip Multiprocessors (CMPs), maintaining cache coherence can account for a major performance overhead. Write-invalidate protocols adapted by most CMPs generate high cache-to-cache misses under producer-consumer sharing patterns. To reduce coherence misses observed in write-invalidate based protocols we may study a dynamic write-update mechanism augmented on top of a write-invalidate protocol. This mechanism is specifically triggered at the detection of a producer-consumer sharing pattern. Secondly, we may extend this adaptive protocol with a bandwidth-adaptive mechanism to eliminate performance degradation from write-updates under limited bandwidth.

Adaptive Cache Coherence Protocol aims at exploring mechanisms that improve shared memory performance by eliminating remote misses and/or reducing the amount of communication required to maintain coherence. Some approaches focuses on improving the performance of applications that exhibit producer-consumer sharing. One is to explore simple hardware mechanism for detecting producer-consumer sharing and then describe a directory delegation mechanism whereby the "home node" of a cache line can be delegated to a producer node, thereby converting 3-hop coherence operations into 2-hop operations. This will extend the delegation mechanism to support speculative updates for data accessed in a producer-consumer pattern, which can convert 2-hop misses into local misses, thereby eliminating the remote memory latency. Both mechanisms can be implemented without changes to the processor. Evaluation of directory delegation and speculative update mechanisms using some server benchmark programs that exhibit producer-consumer sharing using a cycle-accurate execution driven simulator of a future 16-node SGI multiprocessor. The above mechanisms reduce the average remote miss rate by 40%, reduce network traffic by 15%, and improve performance by 21%. Finally, we may use Murphi to verify that each mechanism is error-free and does not violate sequential consistency.

Commodity graphics processing units (GPUs) have rapidly evolved to become high performance accelerators for dataparallel computing. Modern GPUs contain CUDA of arithmetic cores or processing units, capable of achieving TFLOPS for single-precision (SP) arithmetic, and over 500 GFLOPS for double-precision (DP) calculations. We have the following GPU cluster: Two High-density 4U GPU Tower Workstation. Each has the following spec:

· Dual-processor Haswell 6C Xeon E5-2620 v3 – C612 based server, 2.4 GHz, 15M, 8GT/s QPI (9.6 GT/s),

· Motherboard interfacing: 4x PCI-E 3.0 x16 (4 GPUs or 4 MICs), one slot PCI-E 3.0 x8 (1 in x16), and one 1x PCI-E 3.0 x8 (FDR Card).

The two servers are interconnected to each other using an infiniband card and links. Thus, we have two cases: GPUs on one server may communicate directly through PCIe and GPUs residing on different servers must communicate through host and infiniband link. This is expected to have some differences in using (pinned and pageable memory) and communication using MPI is likely to be different. MPI is supported with GPUDirect to work correctly as explained in the Introduction to CUDA-Aware MPI:

MPI communication works fine as far as the communicating GPUs are on the same PCIe. Otherwise (through infiniband) it requires copying the data from Device memory to Host and initiate the send through host-to-host memories.

Different method to communicate between the different GPUs is possible such as by allocating pinned memory on the host. Then, this memory is mapped to each kernel. If any kernel modifies this value, the modification is immediately noticed in all the running kernels on any GPU (shared memory). You may learn about this in this link:

Also, it doesn't seem that this method affected the performance, which is good (almost as if we don't use any communication). I tested the code both with and without it. I got similar execution time. We cannot change the global memory for a kernel only before it starts executing. So to communicate between multiple GPUs, first we do the memory allocation and send the data between them, then we launch the kernels. The method for sending data between two GPUs is

cudaMemcpyPeerAsync( void* dst_addr, int dst_dev, void* src_addr, int src_dev, size_t num_bytes, cudaStream_t stream );

This method is used to invoke a method on the host after a kernel finishes it's execution. Using this we can send data between the GPUs or launch another kernel, for example. I use it to print the result of a kernel after it finishes its execution, in case it succeeds in finding a result.

where /usr/local/lib and /usr/local/lib/openmpi are the folders where the files of the OpenMPI are located on the server. To execute this program this is used:

where 8 is the number of processes we want to start. The only source available for describing CUDA-Aware MPI is this:

11. Data Partitioning on Multicore and Multi-GPU Platforms Using Functional Performance Models

14. Effective Multi-GPU Communication Using Multiple CUDA Streams and Threads (GPUDirect)

15. Use of Multiple GPUs on Shared Memory Multiprocessors for Ultrasound Propagation Simulations

Forward Reservoir Simulation (FRS) is based on linear algebra operations such as solving a linear system Ax=b with multiple Right-Hand Side (m-RHS) equations (multiple Ax=bi to find solution xi for each bi). The use of A=LU factorization some advantages. In this case, the problem is to find matrices L and U that are lower and upper triangular matrices. The steps for solving Ax=b are solving LUx=b by solving LV=b and finding V, and finally solving V=Ux and finding x. The main idea is to record the steps used in Gaussian elimination on A in the places where the zero is produced. The objective is to develop an efficient implementation of Sparse LU factorization solver with m-RHS in CUDA/Library for hepta matrix. A suggest plan is as follows:

(1) Explore the literature on GPU parallel implementation of the LU factorization on GPU including exploring the availability of LU factorization in external libraries like CUBLAS, CuSPARSE, MAGMA, CUSP, Alinea, MKL, etc.

(2) Since A is known to be sparse hepta matrix, we need to explore the optimization of both storage and run time overhead in the LU factorization.

(3) Explore ways to minimize the effect of global synchronization in LU factorization as it has been addressed in the literature.

(4) Using the solution A=LU, optimize the solving of m-RHD by exploring partial computations that can be shared among various RHDs.

Note: LU factorization takes longer time than iterative methods but provides exact solution. For this it is not recommended to be used when approximating Non-Linear systems, where the matrix coefficient varies and accuracy is not a prime objective compared to speed. Thus the main interest is where the matrix remains constant.

An accurate model for computational fluid dynamics (CFD) is through the solving of the Navier–Stokes equations. The Lattice Boltzmann method (LBM) is based on a discrete equations for solving and simulating the flow of a Newtonian fluid using a collision model. It consists of subdividing the simulated 2D or 3D space into volumes, each contains a number of particles set in some predefined directions, and a streaming and collision processes across a limited number of particles. Particles jump (lattice) from one volume to the neighboring ones. The intrinsic particle interactions evince a microcosm of viscous flow behavior applicable across the greater mass. LBM is a major simplification of the original Navier-Stikes CFD for any incompressible fluid such as blood in vessels LBM provides an asymptotic solution which is quite similar to the solution provided by the accurate Navier-Stokes CFD system. The LBM algorithm is based on an outer loop on simulation time, in which there is there are two fundamental phases: (1) Bounce, and (2) Propagation. The project is to write an optimized CUDA program to implement the LBM approach in 3D by considering some boundary conditions as well as some initial conditions. A practical soft book is available with the instructor as well as a sequential simulation program. A proposed plan is to (1) explore papers on implementing LBM on GPUs including Nvidia library on LBM simulation, (2) write optimized CUDA/GPU and C/openMp for LBM simulation, (3) explore algorithm data-layout and parallelization issues on GPU and MIC, (3) simulate some interesting cases in cooperation with some going on research at ARAMCO and provide some 3D visualization of the results, and (4) compare performance with others' published research. The student may search the IeeExplore for papersa on LBM applications on GPUs.

The Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process is then iterated until it converges. This algorithm is a stripped-down version of the Jacobi transformation method of matrix diagonalization. The method is named after German mathematician Carl Gustav Jakob Jacobi.

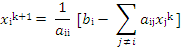
This equation can be used as an iteration formula for each of the unknowns to obtain a better approximation. Note that in the Jacobi method computing xk+1 from xk is a perfectly parallel operation: each new element of xk+1 is computed using the values of xk. This can be achieved by allocating new vector (new_x) to store updated values and then copy this vector into x to be used in the next iteration.

Fortran Code for ADI. From “Automatic data layout for distributed-memory machines”, by Ken Kennedy and Ulrich Kremer. Note loop 2 and 3 can be combined as well as 5 and 6 which produces 4 major loops in the main body.

The Alternating Direction Implicit (ADI) method is a finite difference method for solving parabolic and elliptic partial differential equations. It is most notably used to solve the problem of heat conduction or solving the diffusion equation in two or more dimensions. The traditional method for solving the heat conduction equation is the Crank–Nicolson method. This method can be quite costly. The advantage of the ADI method is that the equations that have to be solved in every iteration have a simpler structure and are thus easier to solve.

ADI implementation consists of four loops L1, L2, L3 and L4. Loop L1 do forward sweep along rows and loop L2 do backward sweep along rows. Loop L3 do forward sweep along columns and loop L4 do backward sweep along columns.

The simplified version of the solver in Ocean simulation is based on the Gauss-Seidel, near-neighbor sweeps (iterations) with a convergence condition (statement 25) is shown below:

Each array is assumed to be an n*n. The drawback of the this algorithm is the Sweep O(n^2) computations and the data dependencies which constrain its parallelization. A good approximation of the above problem is the Red-Black sweeps which covert the above inner two loops to:

(1) A double nested “Red” loop (RL) to repeatedly process even numbered pixels in one row and odd numbered pixels in the next row, etc

(2) A double nested “Black” loop (BL) to repeatedly process odd numbered pixels in one row and even numbered pixels in the next row, etc.