SE301: Introduction to Numerical Methods
Summer 033 Sections 5 and 6
Computer Assignment
Instructor: Dr. Samir Al-Amer
General Instructions:
- The grades of the best five computer assignments are used in computing the computer Assignment grade.
- The grade for each computer assignment is as follows:
2: The program is well-written and the results are correct
1: A series attempt to solve the problem was done but the program is not
complete or the answer is not correct.
0: The assignment was not submitted or submitted too late or no series
attempt to solve the problem was done.
- Write your name and ID # at the top of your program.
- Use MATLAB to solve the computer assignments. Other programming languages may be allowed but prior permission of the instructor is required.
- Late submissions will not be accepted.
- Submit your CHW using the WebCT course account.
Computer Assignment # 1 Due to :_____________
The Nth
order Taylor series expansion of f(x) = sin(x) is given by
![]()
Write a program that computes sin(0.2) using N = 1, 2, 3, 4 and 5. Compute and print the percentage relative error
![]()
Use the built-in sine function to evaluate the true value. Display the result in a tabulated form.
______________________________________________________________________________
Computer Assignment # 2 Due to :_____________
The volume V of a liquid
in a spherical tank of radius r is related to the depth h of the liquid is
given by ![]() . Given h = 1m and V = 0.5m3
. Given h = 1m and V = 0.5m3
Assuming the initial interval [0,2], Write a program that uses Bisection method to determine h with four-decimal-digit accuracy. Your program should display the estimated level.
______________________________________________________________________________
Computer Assignment # 3 Due to :_____________
The trajectory of a ball
thrown by a player is defined in terms of its (x,y)-coordinates.
The trajectory is modeled by ![]() where g = 9.81 and
where g = 9.81 and
![]() . Write a program that implements the Secant method to
determine the initial angle
. Write a program that implements the Secant method to
determine the initial angle ![]() with four-decimal-digit
accuracy so that the ball hit a target with coordinate (40,1). Use 30 and 40
degrees as initial guesses.
with four-decimal-digit
accuracy so that the ball hit a target with coordinate (40,1). Use 30 and 40
degrees as initial guesses.
______________________________________________________________________________
Computer Assignment # 4 Due to :_____________
The node-voltage law was applied to an electrical circuit and the following equations were obtained.
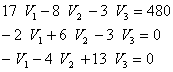
Write a program that implements the Naive Gaussian elimination and use it to solve for the unknowns V1, V2 and V3 and display their values.
Computer Assignment # 5 Due to :_____________
The upward velocity of a
rocket can be computed as  where
where
u : velocity at which burned fuel exit the rocket (u = 2000m/s)
![]() : initial mass of the rocket (
: initial mass of the rocket (![]() = 150000 kg)
= 150000 kg)
q : fuel consumption rate (q = 2600 kg/s)
g : gravitational constant (g = 9.81)
t : time
Write a program that implements the Romberg method of order O(h8) to compute the height the rocket reaches after 30 seconds. Your program should display the Romberg table.
______________________________________________________________________________
Computer Assignment # 6 Due to :_____________
A mathematical model for the area A (in cm2) that a colony of bacteria occupies is given by
![]()
Write a program that uses the Fourth order Runge-Kutta method to compute the area over the interval [0, 5]. Assume the initial area is 0.2 cm2 and use h = 0.05. Your program should display the area after 5 time units and a graph to show the area during the studied interval is also needed.