 (Show the forces acting on the car in the vertical
(Show the forces acting on the car in the vertical
Quiz#3.
Q1.
A ball is thrown at an angle of 600
above the horizontal and with an initial speed of 20.0 m/s. It hits a building 8 m away at a point H meters above the
ground.
x =
vo cosqo t
Therefore,
8 = 20 cos 60o t
Þ
t = 0.8 s
(b) Find the value of H.
y
= vo sin qo t - (1/2) g t2
Þ H = 20 sin 60o *0.8
- (1/2) * 9.8* (0.8)2
\ H = 10.7 m
Q2. A block of mass M = 10.0 kg on a rough inclined plane ( q
= 30o ) is connected by a light string that passes over a
frictionless pulley to a hanging steel ball of mass m , as shown in the figure.
The coefficient of kinetic friction between the block and the surface is 0.20 .
The acceleration of the block down the incline is 1.20 m/s2. Find
(a) the tension in the string, and
(a) M g sinq - T – m M g cos q = M a
Þ T = M g (sinq
-
m cos q ) - M a
T =
10 * 9.8 ( sin 30 – 0.2 cos 30 ) – 10 *1.2
T = 20.0 N
(b) m g - T = m a
Þ m = T / ( g + a)
Þ m = 20/ ( 9.8 +1.2)
kg
Q3.
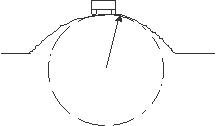
A 2000-kg car passes over a bump in a road that follows the arc of a
circle of radius R = 50 m, as shown in the Figure.
What is the maximum speed the car can have as it passes the highest point
before losing contact with the road?
 (Show the forces acting on the car in the vertical
(Show the forces acting on the car in the vertical
Solution:
m g -
N = m ar ,
where ar =
v2 / R
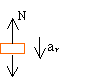
mg
When the car has just lost contact with the road
the normal force is zero. Hence,
when N=0, v = v max
Therefore, m g = m vmax2 / R
Hence, vmax = Ö(g
R) = Ö(9.8
* 50) m/s = 22.1 m/s