16.6 Pendulums
There are two types of pendulums, the simple and the physical.
The applet below shows the motion of a simple pendulum.
Drag the red pendulum bob to a small amplitude (theta) and play. Only the gravity force and its tangential component (component parallel to the path, mg sin q) is shown in the animation. Tension from string has no component in the tangential direction. This net tangential force produces a restoring torque about the pendulum's pivot point, because it always acts opposite the displacement of the bob back towards its equilibrium position (q = 0). Forces in the radial direction produces zero torque about the pivot point.
In the case of small angle oscillations (when sin q
~ q), the restoring torque is: ![]() .
Recognizing that the rotationla inertia is
.
Recognizing that the rotationla inertia is![]() ,
the motion of a simple pendulum can be approximated to a simple harmonic motion
with a period of motion
,
the motion of a simple pendulum can be approximated to a simple harmonic motion
with a period of motion 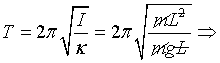
where is the length of the pendulum and is the gravitational acceleration.
A physical pendulum is shown in the figure below.
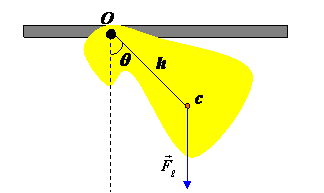
In the case of small amplitude oscillations, the period of motion is given by
where is the rotational inertia of the pendulum about point O (the pivot), m is the mass of the pendulum and h is the distance between the pivot point O and the center of mass of the pendulum C.