![]()
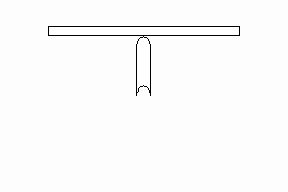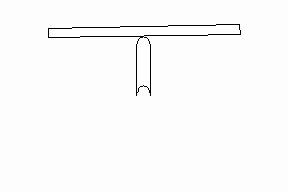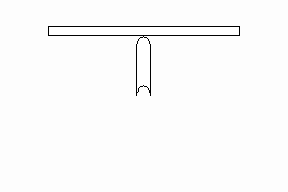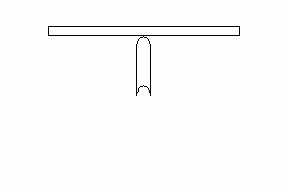
A pen (not really a pen here though, rather a uniform rod) can be balanced on the
fingertip as shown above. You can prove to yourself that this can be done, and it is a
stable equilibrium too.
But when you think about it..(or think along the way that I am going to ask you to think
shortly), you may want to ask why doesn't it tip and fall down, when you give even a very
slight tilt? After all when the rod (let me replace the pen with a uniform rod) is
tilted even slightly to the right (for example) the center of gravity will shift to
the right from the middle (the balancing point). Because we all know that the
gravitational attraction decreases (no matter how small it is) as we move toward the
center of the earth. Or, in other word, the weight of the right side is more than the
weight of the left hand side, which should result in a net torque clockwise!?(about any
point you choose). This should turn it all the way to the right and make it fall. The
slipping along the direction of the tilt may be prevented by the friction force but it
can't stop the tilting furrther down.
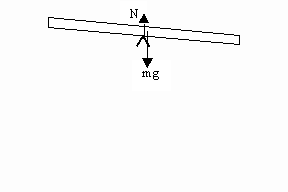
There is one more arguement to say that it should tip, without resorting to the above! As you can see the center of gravity is not at the contact point; it is raised above because of the thickness of the rod (ycg). So again a tilt to the right (for example) should result in a net torque clockwise !? (because of this reason alone). This piece of information, I beleive can act as a clue to solving the problem, if you haven't got it already.
SO the question is: WHERE is the restoring torque coming from, for the pen balanced on your fingertip?