NUCLEAR PROPERTIES

-        Interaction between 50 nucleons is 50 !  terms,  so we have to have a way to study these interactions.

-        mass, radius, density, abundance, decay modes, half lives, reaction modes, cross sections, spin, mag. dipole moment, electric quadrupole moment, excited states.....

-        Static Properties         :  charge, radius, mass ..........

-        Dynamic Properties    :       decay, reaction

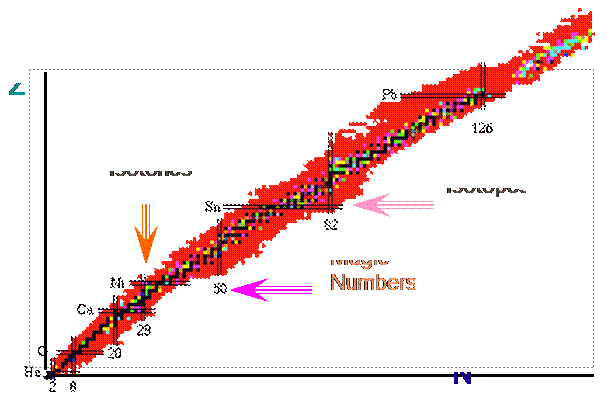
-        108 nuclides (  >1000 if we consider isotopes )

-        Where to find properties of nuclides?!

          (Journals, compiled sources (tables))

-        The nucleus is approximately spherical  Þ  nuclear radius.

-        2 parameters :    1.     Radius        2.     Skin thickness

-        59Co was studied using neutrons (neutron scattering).

-        Why is this diffraction pattern?

          Density is changing in the nucleus so we have a diffraction pattern similar to light going through media of different index of refraction n.

-        Why the diffraction pattern is not so pronounced?! (no sharp surface).

Nuclear density and nuclear potential have the same spatial dependence.             

     we are measuring distribution of nuclear charge.

The Distribution of Nuclear Charge

-           Radiation Scattering   Shape of the object

            Dimension of the object

-           Beams of electrons with energies 100 MeV to 1 GeV are used.

-           Diffraction patterns are analyzed and

-           Initial wave function

-           Electron can be considered as a free particle

-           After scattering of the electron

            and wave function

-           The potential is

-           Transition probability  where

            =

-          

-          

            Substituting and integrating over r we get we get the normalized result

-          

             is the distribution of the nuclear charge.

-          

      for elastic scattering

q is a function of the scattering angle

-           F(q) =  form factor    using Fourier Transfer

-           Notice that the density is almost constant for all nuclei.

-           # of nucleons/unit volume      constants.

-           t is distance from 90% of  to 10% of

-           Root mean square radius < r² > ==(R²) for a uniformly charged sphere.

-           See other ways of calculating nuclear charge radius in Krane.

-                   

r1 = density at small values of  r

                      Re = r    at  r = r1 / 2

                      t = surface thickness

-        Charge density & matter density.

-        It is found that nuclear matter density is the same for all nuclei aside from surface effects.

-        t   2.4 fm

-        Re   1.07 A 1/3  =  r0 A 1/3    fm  = mean electromagnetic radius

-        nuclear potential radius

          R  1.22  A 1/3    fm

THE DISTRIBUTION OF NUCLEAR MATTER

-           Interaction between two nuclei due to nuclear force

                   Nuclear radius rather than Coulomb radius.

-           Consider the scattering of  particles  from  (Rutherford Scattering).

-           Particles should have enough energy to overcome the Coulomb potential    break down of Rutherford’s formula see Fig. 3.11.

-           Another method of determining the nuclear radius is -decay.

-           -particle must escape the nuclear potential to the Coulomb potential.

-           -decay probabilities can be calculated using Schrödinger’s equation.

-           Comparison with measured values  R

-           The charge and matter radius of nuclei are nearly equal to within about 0.1f.

NUCLEAR MASS

-        Nucleus has 99.97% of the mass of an atom.

-        Old scale (O16) new scale (C12)

            C12 = 12.000000 u

                  E = 931.48 MeV

            See tables at the end of KRANE & ENGE practice with a nucleus.

            Neutron       =       1.008665 u

            Proton         =       1.007277 u

          What happened to the rest of the mass for a nucleus like  for example?

MASS AND ABUNDANCE OF NUCLIDES

-                     Although we need to use nuclear masses in nuclear reactions and decays, tables list the values of neutral atoms only  we need a correction.

-                     The Binding Energy in the nuclear is large.

-                     For a typical nucleus B.E  8 M.eV  8 * 10^-3 of total mass

(for atomic B.E  1.4*10^-8)

-                     For quarks the B.E is about 0.99 of the total energy, so 3 quarks of total energy of ~ 300 Ge combine to produce a nucleon of rest energy 1 GeV.

-                     So it is not possible to separate the discussion of rest mass from binding energy.

-                     Experimentally how do we measure nuclear masses?

-                     The old and precise method is through Nuclear Mass Spectrometry.

-                     Neighboring isotopes differ in mass by approximately 1%.

-                     Mass Spectroscopes can measure masses to a precision of 10^-6.

-                     A Mass Spectrograph has:

Ion Source                    Velocity Selector           Momentum Selector

          electromagnetic field      uniform magnetic field

qE = qvB will pass  v = E/B_s

F_r= F_B

-        For accuracy we measure the difference between two nearly equal masses (mass doublets).

NUCLIDE ABUNDANCES

-        We can use the mass spectrometer to find the nuclide abundance also by varying E or B (see Fig. 3.14)

SEPARATED ISOTOPES

-                     If we set the Mass Spectrometer on a certain mass, we can produce large quantities of it to do experiments. Oak Ridge Nat. Lab sell these isotopes.

LASER ISOTOPE SEPARATION

-      Set one laser to excite only certain atoms (How).A second laser will ionize these atoms only and can be collected using an electric field (Fig. 3.15).

BINDING ENERGY

                            (1)

          Or

                         (2)

          What happened to the electron mass in (1) and B of electrons

            = Binding energies for electrons    10 - 100 keV

          Neutron Separation Energy   (How to find it)

          Proton Separation Energy Sp

Þ      Similar to atomic ionization energies

-        If we plot A vs B/A we notice the  following

          1. The curve is relatively constant except for light nuclei.

          2. B/A   8 MeV   to within 10%

          3. At A = 60 nuclei are most tight

 hence we gain energy by either assembling lighter nuclei into heavier ones (fusion) or by breaking heavier nuclei into lighter nuclei (fission).

Þ      Homework  (check the above statement)

Fission and fusion can yield energy

-        Trying to understand this curve led to semiempirical mass formula.

            B/A  constant       Þ      B = av A 

-        We would expect B µ     (A-1)   (Why)

          Þ        nucleon interact only with their closest neighbors.

          Þ        short distance effect  ( for the nuclear force )

-        B = av A is an overestimate because nucleons on the surface don't contribute the same as inner nucleons, so we have to subtract a term proportional to Surface Area ~  

          (why    & Surface Area is  µ  R2)

So

          B =

          We also need a term µ Coulomb interaction or Z (Z-1), why ?  (since each proton repel all others)

So

          B =  -  ac Z (Z-1) / A1/3    (why “ – “for Coulomb)

-        We also need a term that favors nuclei along the line Z=N or Z = A/2

-        -

      The further away a nucleus is from Z = N the less bound it is.

-        From observing nuclei in nature they found that there are only 4 stable nuclei with odd N and Z

           and 167 stable nuclei with even N and Z.

Þ      There must be a pairing term d ( other forms exist )

          Where

                      ì    ap A-3/4       for even N and Z

                      ï

            d =     í     0               for odd A (even Z and odd N or vice versa)                 ï

                      î - ap A-3/4       for odd N and Z

-               

               , 

               ,  

          M(Z, A) = Z m_H + N m_n – B (Z, A)/ c²

-         For constant A This is an equation of a parabola ( See Fig 3.18)

-         We can find the minimum by differentiating ¶M / ¶Z = 0