An isolated conductor with a spherical cavity has an
excess charge of - 13 nano-Coulomb. Then, a charge of
- 5 nano-Coulomb is placed at the center of the cavity.
What will be the charge on the outer surface of the conductor ?
a - 13 nano-Coulomb
b - 8 nano-Coulomb
c + 5 nano-Coulomb
d - 18 nano-Coulomb
e + 8 nano-Coulomb
==============================================
Question 2
An isolated conductor of arbitrary shape has a net
charge of +20*10**(-6) C. Inside the conductor is a
cavity within which is a +5*10**(-6) C point charge.
Find the charges on the cavity wall and on the outer
surface of the conductor.
a -5*10**(-6) C , +25*10**(-6) C
b +5*10**(-6) C , -25*10**(-6) C
c -20*10**(-6) C , +25*10**(-6) C
d -5*10**(-6) C , +20*10**(-6) C
e -5*10**(-6) C , +15*10**(-6) C
==============================================
Question 3
An isolated conductor of arbitrary shape has a net charge of
-15*10**(-6) C. Inside the conductor is a cavity within which
is a point charge q=-5.0*10**(-6) C. What is the charge on the
cavity-wall, q(in), and what is the charge on the outer surface
of the conductor, q(out)? [See figure (3)].
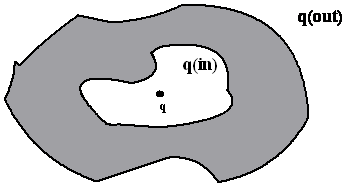
a q(in) =-5.0*10**(-6) C; q(out) = -15*10**(-6) C.
b q(in) = 5.0*10**(-6) C; q(out) = -20*10**(-6) C.
c q(in) =-5.0*10**(-6) C; q(out) = -10*10**(-6) C.
d q(in) = 5.0*10**(-6) C; q(out) = -10*10**(-6) C.
e q(in) = 5.0*10**(-6) C; q(out) = -15*10**(-6) C.
==============================================
Question 4
Figure 3 shows two infinitely long rods carrying uniform
linear charge densities lambda1 and lambda2. If the net
electric field at point A is zero, then the ratio
lambda2/lambda1 is:

a 0.71
b 2.3
c 2.7
d 1.7
e 1.4
==============================================
Question 5
The cube in figure 3 has edge lengths of 2.00 m and is
oriented as shown in a region in which a uniform electric
field exists.
The electric field is given by: (-5.00 i + 8.00 k) N/C,
where i and k are unit vectors parallel to the x-axis
and z-axis respectively.
Find the electric flux through the right face (shaded)
of the box.

a -10.0 N.m**2/C
b zero
c +6.00 N.m**2/C
d +16.0 N.m**2/C
e +26.0 N.m**2/C
==============================================
Question 6
An electron is shot directly toward the center of a large metal
plate that has excess negative charge with surface charge density
2.0*10**(-6) C/m**2. If the initial kinetic energy of the
electron is 200 eV and if the electron is to stop just as it
reaches the plate, how far from the plate must it be shot?
a 0.5 mm.
b 0.6 mm.
c 0.9 mm.
d 0.4 mm.
e 0.2 mm.
==============================================
Question 7
A point charge of +4.0 micro-C lies at the center of a hollow
spherical conducting shell that has a net charge of -13.0
micro-C. If the inner radius of the shell is 2.0 cm and the
outer radius is 3.0 cm, then the ratio between the charge
density on the inner surface to the charge density on the
outer surface is:
a 1 : 1.
b -1 : 2.
c -1 : 1.
d 1 : 2.
e 4 : 1.
==============================================
Question 8
Two long, charged, concentric cylindrical shells have
radii 3.0 and 6.0 cm.
The charge per unit length is -2.00*10**(-6) C/m on the
inner cylinder and +5.00*10**(-6) C/m on the outer
cylinder. Find the electric field at r = 4.0 cm, where
r is the radial distance from the common central axis.
a 9.00*10**5 N/C radially inward
b 9.00*10**5 N/C radially outward
c 22.5*10**5 N/C radially inward
d 13.5*10**5 N/C radially inward
e 13.5*10**5 N/C radially outward
==============================================
Question 9
A point charge of 2.0 micro-C is placed at the center of a cube
50 cm on edge. What is the flux through the bottom surface?
a -2.8*10**4 N*m**2/C.
b 1.1*10**5 N*m**2/C.
c 1.7*10**4 N*m**2/C.
d 3.8*10**4 N*m**2/C.
e -5.6*10**4 N*m**2/C.
==============================================
Question 10
A closed cylinder whose main axis is along the x-axis
is shown in figure 2. It is placed in a uniform electric
field of magnitude 200 N/C pointing in the negative x-axis.
The cylinder has a cross sectional area of 12.5 cm**2 and
a length of 6.0 cm.
The fluxes through faces I, II and III are respectively:

a 0.25 , zero , - 0.25 N*m**2/C
b - 0.25 , 0.25 , - 0.25 N*m**2/C
c zero , -0.25 , zero N*m**2/C
d zero , 0.25 , zero N*m**2/C
e - 0.25 , zero , 0.25 N*m**2/C
==============================================
Question 11
A cube, as in figure (6), has an edge length of 3.00 m in a
region of a uniform electric field given by the equation:
E = (- 5.00 j + 6.00 k) N/C,
where i, j, and k are the unit vectors in the directions of
x, y, and z respectively.
Find the electric flux through the top face (shaded).

a - 45 N*m**2/C.
b 30 N*m**2/C.
c 45 N*m**2/C.
d - 30 N*m**2/C.
e Zero.
==============================================
Question 12
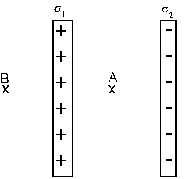
Figure 4 shows two large, parallel, non-conducting
sheets, each with fixed uniform charge density:
sigma1 = + 2.2*10**(-6) C/m**2
sigma2 = - 4.3*10**(-6) C/m**2.
The ratio of the magnitude of the electric field
at point A to that at point B is:
a 4.4
b 3.1
c 1.5
d 0.6
e 2.2
==============================================
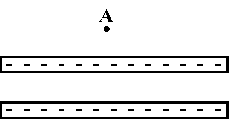
Question 13
Figure 4 shows cross-sections through two large, parallel
non-conducting sheets with identical distributions of
negative charge. The surface charge density for each
sheet is 7.00*10**(-15) C/m**2.
What is the electric field at point A ?
a 3.96*10**(-4) N/C downward
b 3.96*10**(-4) N/C upward
c 7.91*10**(-4) N/C upward
d 7.91*10**(-4) N/C downward
e 0
==============================================
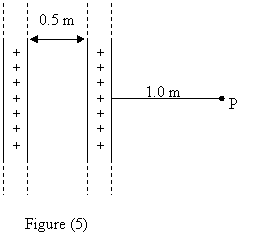
Question 14
For the two infinite dielectric sheets, see figure (5), find
the magnitude of the electric field at a point P. Consider
that each sheet has a positive surface charge density of
10**2 C/m**2.
a 2.2*10**13 N/C.
b 0.5*10**13 N/C.
c 1.7*10**13 N/C.
d Zero.
e 1.1*10**13 N/C.
==============================================
Answers
1 d
2 a
3 b
4 e
5 b
6 c
7 a
8 a
9 d
10 a
11 a
12 b
13 d
14 e