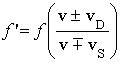Summary of Chapter 18
![]()
1. Sound waves are
longitudinal; that is the particles of the medium move parallel to the direction of
motion of the wave.
The
velocity of sound in different media is given by;
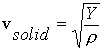 where Y is the Young
modulus
where Y is the Young
modulus ![]()
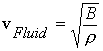 where B is the Bulk
modulus
where B is the Bulk
modulus ![]()
vair
= 343 m/s at a temperature of about 20 oC and vvacuum = 0
2. A harmonic sound wave can be
described by a displacement wave
or a pressure wave.
The
displacement wave for a harmonic sound wave is given by;
![]()
where s(x,t) is the
diplacement of the particles in the medium, k is the wave
number, w is the angular frequency,
and Sm is the displacement amplitude.
The
pressure wave is given by;
![]()
Where
![]()
DPm is the pressure amplitude
and r is the density of the medium and v is te speed of sound in the medium.
3. Interference of sound waves
The relationship between the difference in path and
the phase difference between the two sound waves at the location of a listener
is
![]()
DL is the path length difference between the two sound
waves.
2 Cases:
a)
Constructive interference (maximum sound) DL = 0,
l, 2l, 3l
Þ ![]() for n = 0, 1, 2, 3, 4,
for n = 0, 1, 2, 3, 4,
b)
Destructive interference (minimum sound) Dr = 0, l/2, l, 3l/2 .
Þ ![]() for n = 1, 3, 5, 7,
for n = 1, 3, 5, 7,
4. The power transmitted in a harmonic
sound wave is given by;

The intensity of a sound wave I is
defined as 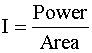 (W/m2)
(W/m2)
Þ ![]()
Since the intensity of sound varies between
10-12 W/m2 to 1 W/m2 we define a new quantity
called sound intensity level b as
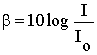
where Io = 10-12 W.m2 is the reference
intensity.
The units for b is dB (Decibel). Now b varies between 0 and 120 dB.
For spherical sound waves, the intensity is
given by;
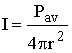
(r: distance between the source and the point
where we want to measure the intensity).
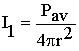 and
and 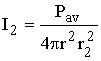 Þ
Þ
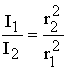
- Standing Waves in air columns (pipes)
Sound sources can be used to produce longitudinal standing waves in air columns.
2 Cases:
a)
pipe
open at both ends: The resonances occur for
L = n l/2 for
n = 1, 2, 3, 4, ..
since v = lf Þ
f = (n v)/2L for n = 1, 2, 3, 4, ..
where v is the speed of sound waves
b)
pipe
closed at one end: the resonances occur when
L = n l/4 for n = 1, 3, 5, 7,
Þ f = n v/4L
for
n = 1, 3, 5, 7,
6.
The Doppler Effect
The Doppler effect
is the change in frequency f heard by a detector whenever there is relative motion between a source and a
detector. There are 8 cases described as follows:
Detector Source Equation
D S 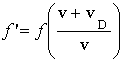 Detector moving toward
stationary source
Detector moving toward
stationary source
![]()
![]() D S
D S 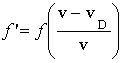 Detector moving away
from stationary source
Detector moving away
from stationary source
![]() D S
D S 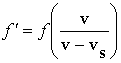 Source moving away from
a stationary detector
Source moving away from
a stationary detector
![]() D S
D S  Source moving toward a stationary
detector
Source moving toward a stationary
detector
![]()
![]()
![]() D S
D S 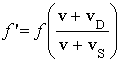 Detector approaching
and source is moving away
Detector approaching
and source is moving away
![]()
![]() D S
D S 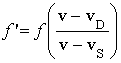 Source approaching and
detector moving away
Source approaching and
detector moving away
![]()
![]()
![]() D S
D S 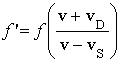 Source and detector are
both approaching
Source and detector are
both approaching
![]()
![]() D S
D S  Source and detector
are both moving away
Source and detector
are both moving away
InGeneral