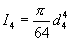- The shaft at the gear shall not deflect more than 0.001"
- The shaft slope through the bearings shall not exceed 1°
![]()
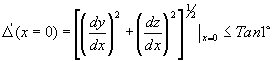
and
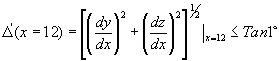
The following analysis explains the successive integration (double integration) method. It shows how to find both the deflections and slopes in the vertical direction (y-axis).
You are required to complete the required calculations and to find the slopes and deflections in the horizontal direction (z-axis) by yourself.
In the double integration method, the following equations form the basis for the analysis:
Load Equation |
|
Shear Equation |
|
Moment Equation |
|
Slope Equation |
|
Deflection Equation |
|
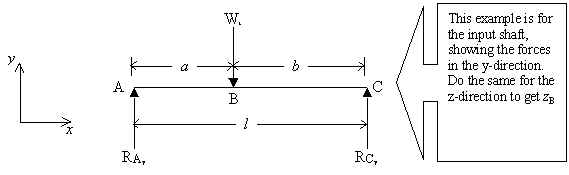
- For 0 ≤ x ≤ A
- For A ≤ x ≤ A+B
- For A+B ≤ x ≤ A+B+C
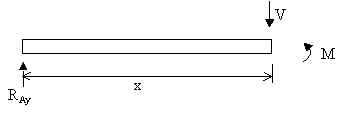
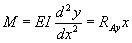
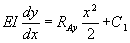 ………………….. eqn. 1
………………….. eqn. 1
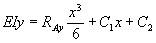 ………………….. eqn. 2
………………….. eqn. 2
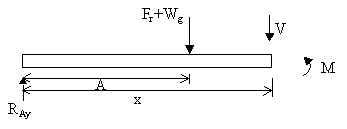
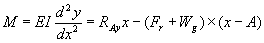
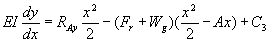 ………………….. eqn. 3
………………….. eqn. 3
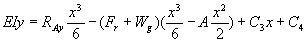
………………….. eqn. 4

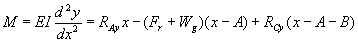
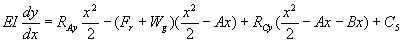
………………….. eqn. 5
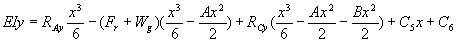
………………….. eqn. 6
Equations 1 through 6
above involve 6 unknowns (C1, C2, C3, C4, C5 & C6), and hence, 6 boundary
conditions are needed to solve for the 6 unknowns. The 6 boundary conditions are as
follows:The 6 boundary conditions above are applied to the 6 equations (equations 1 through 6 ) and the resultant equations are solved simultaneously to find the 6 unknowns (C1 through C6). |
Note:
The equations can be solved easily using any of the available math software like
Mathcad, Maple, Mathematica or Matlab
Now, to solve for the deflection under the gear in the y-direction, substitute for C1 and C2 in equation 2 to obtain:
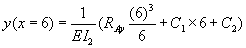
where:
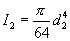
To find the slope of the shaft at the 1st bearing, substitute for C1 in equation 1 to obtain:
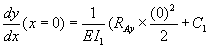
where:
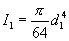
To find the slope of the shaft at the 2nd bearing, substitute for C3 in equation 3 to obtain:

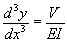
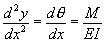
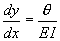
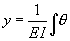
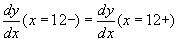 ……………. B.C. # 6
……………. B.C. # 6