Section 11.5 Inferences Concerning the Regression Coefficients
Confidence Interval for b
, the slope parameter
A (1-a)100% confidence interval for the parameter b in the regression line mY|x = a + bx is
![]()
where ![]() is a value of the t-distribution
with n-2 degrees of freedom
is a value of the t-distribution
with n-2 degrees of freedom
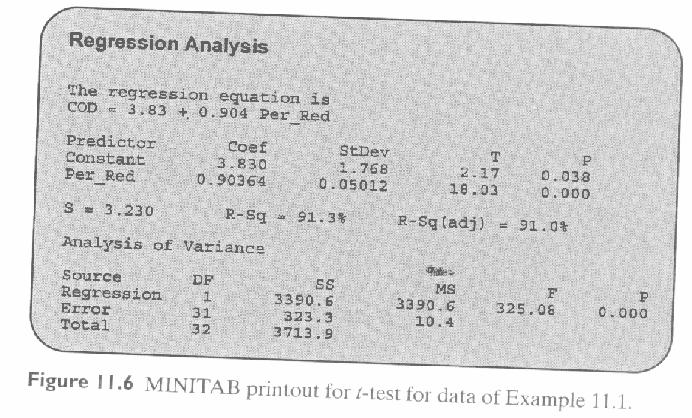
Example 11.2

Hypothesis testing on the slope parameter, b
To test the null hypothesis Ho:b = bo against any suitable alternatives,
use t-distribution with n-2 degrees of freedom to define the critical region, and the following test statistic
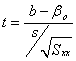
Example 11.3

Minitab Example:
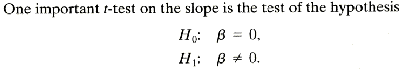
![]()
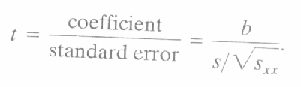
Statistical Inference on the intercept
Confidence Interval for a
, the intercept parameter
A (1-a)100% confidence interval for the parameter a in the regression line mY|x = a + bx is
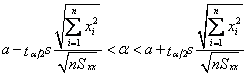 or
or

where ![]() is a value of the t-distribution
with n-2 degrees of freedom
is a value of the t-distribution
with n-2 degrees of freedom
Example 11.4

Hypothesis testing on the intercept parameter, a
To test the null hypothesis Ho: a = ao against any suitable alternatives,
use t-distribution with n-2 degrees of freedom to define the critical region, and the following test statistic

Example 11.5
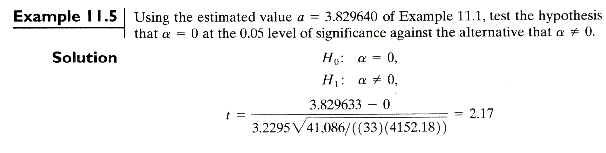
df=33-2=31, P-value =
![]()
From Table A.4 directly, P-value < 0.05. So, the null hypothesis of zero intercept is rejected at 0.05 level of significance.
A measure of quality of fit: Coefficient of
Determination, R2
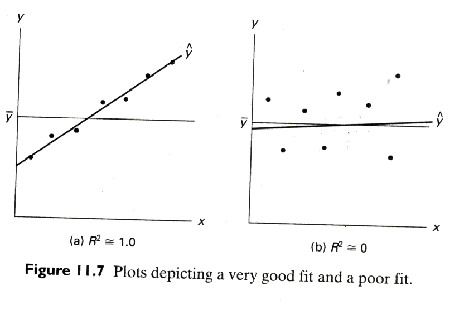
Coefficient of Determination, R2 = proportion of total variability in the dependent variable Y explained by the fitted model.
TSS = SSR + SSE
Coefficient
of Determination, ![]()
R2 = 1.0 if fit is perfect
R2 = 0.0 if fit is poor
Section 11.6 Prediction
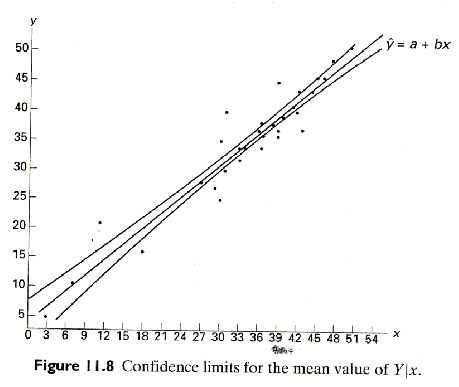
Confidence Interval for ![]() , the mean response
, the mean response
A (1-a)100% confidence
interval for the mean response ![]() in the regression line mY|x = a
+ bx is
in the regression line mY|x = a
+ bx is

where ![]() is a value of the t-distribution
with n-2 degrees of freedom
is a value of the t-distribution
with n-2 degrees of freedom
Example 11.6


Prediction Interval for ![]() , the future value of a response
, the future value of a response
A (1-a)100% prediction
interval for a single response ![]() in the regression line mY|x = a
+ bx is
in the regression line mY|x = a
+ bx is

where ![]() is a value of the t-distribution
with n-2 degrees of freedom
is a value of the t-distribution
with n-2 degrees of freedom
Example 11.7
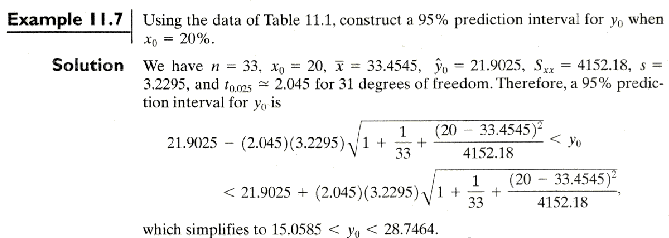
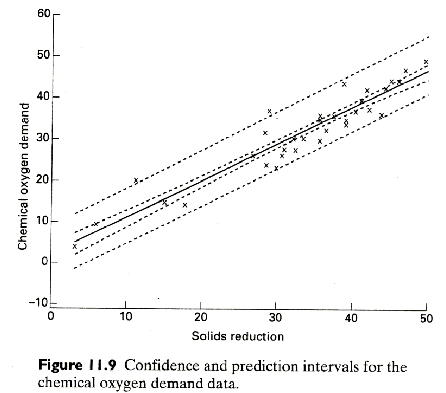
Section 11.11 Simple Linear Regression
Case Study
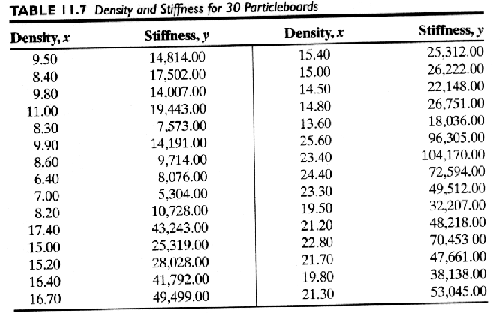
![]()
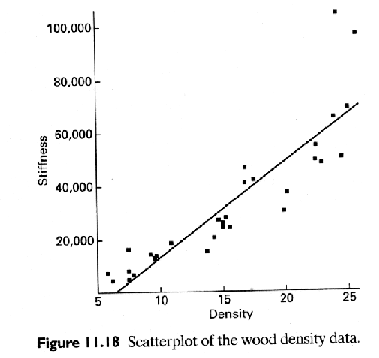
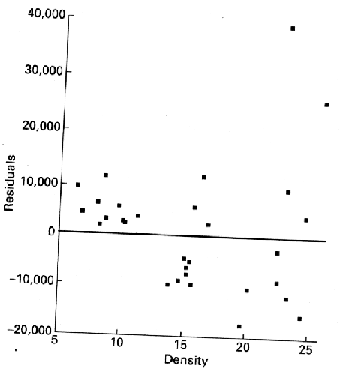
![]()
A more complicated model may be more appropriate
![]()
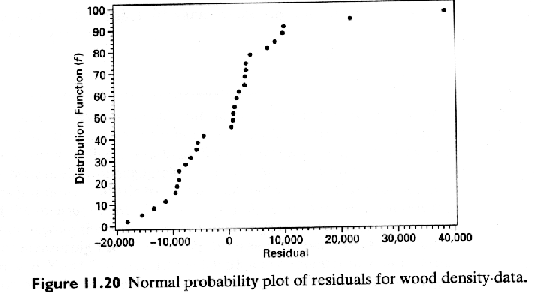

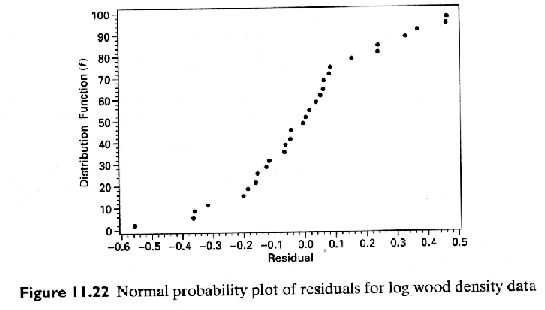
The higher R2 value would suggest that the transformed model is more appropriate.
Section 11.12
Correlation
Correlation coefficient
The measure r of linear association between two variables X and Y is estimated by the sample correlation coefficient r, where

-1 < r < 1
r = 1.0 or –1.0 perfect linear relationship
r = 0.0 no linear relationship
Sample coefficient of determination
![]()
represents the proportion of the variation in TSS explained by the regression of Y on x, namely, SSR.
Example 11.10

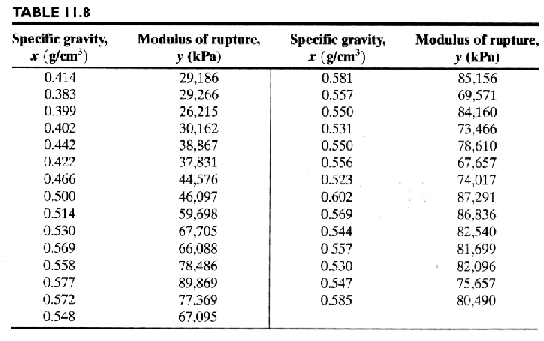
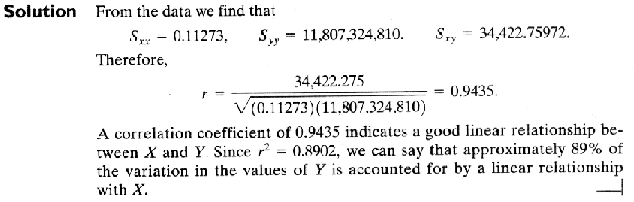
Hypothesis testing on the correlation coefficient, r
To test the null hypothesis Ho: r = ro against any suitable alternatives,
We can use t-distribution with n-2 degrees of freedom to define the critical region, and the following test statistic
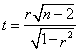
but this test has problem when r values close to -1 or 1
However, a more general test is given by
![]() the
approximate normal distribution with mean
the
approximate normal distribution with mean ![]() and variance
and variance ![]() .
.
We can use the standard normal to define the critical region, and the following test statistic
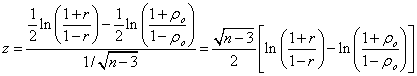
Example 11.11
![]()

Example 11.12
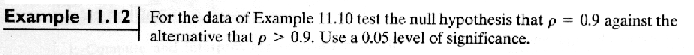
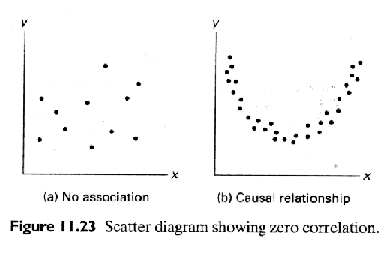
Important: Correlation is a measure of linear relationship, so r = 0 does not necessarily mean there is no relationship between two variables.