CHAPTER SIX

Statistical Estimation

 

 

 6.1 Point Estimation

 

The following table contains some of the well known population parameters and their point estimates based on a random sample.

 

                        Table 1 Population parameters and their corresponding sample estimates

 

Population

Sample

Mean

Variance

Proportion

 

6.2 Confidence Interval Estimation for the Population Mean

 

Point estimates may be far away from the true parameter if the estimators have large variances. So we want to estimate parameters by confidence intervals that consider the variability and the sampling distribution.

 

Confidence Interval Estimation on the Mean of a Normal Population, Variance Known

A  confidence interval for mean is given by:

or

 

where is the  is the  percentile of the standard normal distribution.

 

Example 6.1 The average zinc concentration recovered from a sample of zinc measurements in 36 different locations is found to be 2.6 grams per millimeter. Find a 95% confidence interval for the mean zinc concentration in the river. Assume that the population standard deviation is 0.3 (Walpole, Myers, Myers and Ye, 2003, pp. 236-237).

 

Solution Since the population standard deviation , we assume that zinc measurements follow a normal distribution . With ,  so that a 95% CI for  is given by

 

, i.e.

                                 

Large Sample Confidence Interval for the Population Mean

A % confidence interval (CI) for the population mean is given by

                       

Example 6.2 A meat inspector has randomly measured 30 packs of acclaimed 95% lean beef. The sample resulted in the mean 96.2% with the sample standard deviation of 0.8%. Find a 98% confidence interval for the mean of similar packs (Walpole, R. E. et. al, 2002, 236-237).

 

Solution A 98% CI for  is given by

, i.e.

 

An Experiment for Large Sample Confidence Interval

One hundred samples each of size 30 have been drawn from an exponential distribution with mean 2, and 95% confidence interval have been calculated for each sample using Statistica.  The sample mean, LCL (Lower Confidence Limit) and UCL (Upper Confidence Limit) are given in Table 6.2. The interval that contains the true mean 2 is followed by a Y, otherwise by N.

 

     Table 6.2 Large Sample Confidence Intervals by Statistica

Sample

Mean

LCL

UCL

Y/ N

NewVar1

2.1790

1.5788

2.7792

Y

NewVar2

1.9778

1.1719

2.7836

Y

NewVar3

2.5806

1.6660

3.4951

Y

NewVar4

2.1161

1.2453

2.9868

Y

NewVar5

1.9929

1.2145

2.7714

Y

NewVar6

2.3214

1.4795

3.1633

Y

NewVar7

2.0379

1.3489

2.7271

Y

NewVar8

2.4378

1.3352

3.5405

Y

NewVar9

2.1490

1.3694

2.9287

Y

NewVar10

1.7582

1.2117

2.3047

Y

NewVar11

1.7566

1.1819

2.3312

Y

NewVar12

2.0279

1.1847

2.8710

Y

NewVar13

2.0105

1.2118

2.8094

Y

NewVar14

1.8774

1.1075

2.6473

Y

NewVar15

1.7119

1.1854

2.2386

Y

NewVar16

1.8232

1.1598

2.4867

Y

NewVar17

2.7502

1.8101

3.6902

Y

NewVar18

2.1466

1.2467

3.0465

Y

NewVar19

1.9332

1.2452

2.6212

Y

NewVar20

2.0821

1.3345

2.8297

Y

NewVar21

1.4457

0.9776

1.9138

N

NewVar22

1.7582

1.2355

2.2809

Y

NewVar23

1.9975

1.2987

2.6962

Y

NewVar24

1.7588

0.8082

2.7094

Y

NewVar25

1.8509

1.1329

2.5689

Y

NewVar26

1.3934

0.8597

1.9271

N

NewVar27

1.8494

1.2896

2.4092

Y

NewVar28

1.8064

1.1125

2.5002

Y

NewVar29

2.3428

1.5917

3.0939

Y

NewVar30

1.8725

1.2316

2.5134

Y

NewVar31

1.9489

1.2072

2.6906

Y

NewVar32

1.8292

0.9996

2.6588

Y

NewVar33

1.4579

1.0048

1.9111

N

NewVar34

2.1429

1.2687

3.0173

Y

NewVar35

2.0964

1.0399

3.1528

Y

NewVar36

1.9006

1.2708

2.5310

Y

NewVar37

2.0545

1.2358

2.8732

Y

NewVar38

2.0777

1.1938

2.9616

Y

NewVar39

2.1266

1.2661

2.9872

Y

NewVar40

2.0915

1.3087

2.8744

Y

NewVar41

2.3041

1.3396

3.2686

Y

NewVar42

1.5656

0.9763

2.1549

Y

NewVar43

2.7001

1.6032

3.7970

Y

NewVar44

2.3216

1.1147

3.5285

Y

NewVar45

2.2822

1.4709

3.0935

Y

NewVar46

1.5049

0.9677

2.0423

Y

NewVar47

2.3985

1.5324

3.2645

Y

NewVar48

2.2272

1.1277

3.3267

Y

NewVar49

2.3145

1.5413

3.0877

Y

NewVar50

1.8669

1.0764

2.6576

Y

NewVar51

1.6973

0.9257

2.4689

Y

NewVar52

1.4834

0.9449

2.0219

Y

NewVar53

2.1219

1.4426

2.8013

Y

NewVar54

2.0054

1.3186

2.6923

Y

NewVar55

2.2493

1.3744

3.1243

Y

NewVar56

1.7336

1.1152

2.3519

Y

NewVar57

1.7186

1.0996

2.3376

Y

NewVar58

1.2960

0.7826

1.8095

N

NewVar59

2.3322

1.4760

3.1884

Y

NewVar60

1.9447

1.2595

2.6299

Y

NewVar61

2.3604

1.5601

3.1608

Y

NewVar62

2.8159

1.9349

3.6969

Y

NewVar63

2.4363

1.5238

3.3489

Y

NewVar64

2.1681

1.3227

3.0135

Y

NewVar65

1.6833

1.1838

2.1828

Y

NewVar66

2.2904

1.3307

3.2501

Y

NewVar67

1.6014

0.8826

2.3203

Y

NewVar68

1.6944

1.19022

2.1986

Y

NewVar69

2.2796

1.5889

2.9702

Y

NewVar70

1.7836

1.2667

2.3005

Y

NewVar71

1.5878

1.0871

2.0885

Y

NewVar72

2.6200

1.6938

3.5463

Y

NewVar73

1.6798

0.8418

2.5177

Y

NewVar74

1.2743

0.9735

1.5749

N

NewVar75

2.1606

1.3443

2.9769

Y

NewVar76

1.3105

0.7919

1.8289

N

NewVar77

2.1495

1.3038

2.9952

Y

NewVar78

2.2101

1.4763

2.9438

Y

NewVar79

2.4033

1.4772

3.3293

Y

NewVar80

1.8017

1.3024

2.3009

Y

NewVar81

1.7591

1.1780

2.3401

Y

NewVar82

2.0183

1.3443

2.6923

Y

NewVar83

1.5494

0.9228

2.1761

Y

NewVar84

2.4460

1.5185

3.3736

Y

NewVar85

1.7547

1.2521

2.2572

Y

NewVar86

1.9683

1.1867

2.7499

Y

NewVar87

1.7297

1.2564

2.2032

Y

NewVar88

1.9599

1.3147

2.6051

Y

NewVar89

2.0622

1.4277

2.6968

Y

NewVar90

1.8086

1.2125

2.4047

Y

NewVar91

1.3786

0.7675

1.9897

N

NewVar92

1.9505

1.2360

2.6649

Y

NewVar93

1.8886

1.1770

2.6001

Y

NewVar94

2.0094

1.3489

2.6699

Y

NewVar95

2.1840

1.4007

2.9673

Y

NewVar96

1.8148

1.2167

2.4129

Y

NewVar97

1.8457

1.2152

2.4762

Y

NewVar98

2.2048

1.1911

3.2184

Y

NewVar99

2.5565

1.6199

3.4932

Y

NewVar100

1.9319

1.1761

2.6877

Y

 

 

We observe that 93% of the interval envelope or trap the true mean , whereas the theory says that 95 out of 100 should include . This however, is a fairly good agreement between theory and application. You may draw 100 samples each of  size 50, calculate 100 confidence intervals and see the difference!

 

Confidence Interval on the  Mean of a Normal Population, Variance Unknown

A % confidence interval (CI) for the population mean  is given by

          

 

where  is the  percentile of  student  distribution with degrees of freedom.

 

Example 6.3 The contents of 7 similar containers of sulfuric acid are 9.8, 10.2 10.4, 9.8, 10.0, 10.2 and 9.6 liters. Find a 99% confidence interval for the mean of all such containers, assuming an approximate normal distribution (Walpole, R. E. et. al, 2002, pp. 236-237)

 

Solution For 6 degrees of freedom, using Appendix A3. A 99% confidence interval for the mean  is given by

 

, i.e.

 

6.3 Computing Confidence Intervals Using Statistica

 

Normal Confidence Interval

To compute a z-interval, we compute  from the probability calculator, and find  and  (if necessary) by Descriptive Statistics and then compute the z-interval manually using the appropriate formula.  Alternatively, macros can be written to do the task, but that will not be considered here. On the other hand, if we wish to compute a  normal confidence interval, we need to find by the use of Statistica as shown in Chapter 4. Next, we find the value of and  as we did in Chapter 2.  Then we use the formula given earlier in  this chapter to find the confidence interval, see Examples 6.1 and 6.2.

 

Student t  Confidence Interval

The calculation of confidence intervals in the package is based on the assumption that the variable is normally distributed. No matter what the sample size is, Statistica always gives a t-interval. Suppose that we need to find 99% t-interval for the population mean in Example 6.3.  Follow the steps:

1.      Enter the sample values in an empty column, say VAR1

2.      Statistics / Basic Statistics / Tables

3.      Descriptive Statistics / OK

4.      Variables / VAR1 / OK

5.      Advanced (under Variation, moments check Conf. Limits for means)

6.      Enter 99 for Interval

7.      Summary  

                                               

 

The following scroll sheet of results will be displayed by Statistica:

 

Confidence

– 99.000%

Confidence

+ 99.000%

9.6037

10.3963

 

The interval [9.6037, 10.3963] is the 99% confidence interval for mean content of sulfuric acid in a container (Confer with the calculation by pocket calculator as done in Example 6.3).

 

6.4 Confidence Interval Estimation of the Difference Between Two  

       Population Means

 

Confidence Interval for the Difference between the Means of Two Independent Normal  Populations, Variances Known

 

A  CI for  is given by

.

 

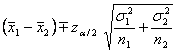Example 6.4: An experiment was conducted with two types of engines, . Gas mileages in miles per gallon were measured. Fifty experiments were conducted using engine Type A and 75 experiments were done for Engine Type B. The gasoline used and other conditions were held constant. The average gas mileage for Engine was 42 miles per gallon and that for Engine was 36 miles per gallon. Find a 96% confidence interval for the difference between the gas mileages for the two types of engines. Assume that population standard deviations of gas mileages are 6 and 8 for engines  (cf. Walpole, et.al, 2003, 236-237)

 

Solution With , a 96% CI for  is given by

,  i.e. .

 

 

Large Sample Confidence Interval for the Difference Between the Means of Two Independent Populations, Variances Unknown

A  confidence interval (CI) for the difference between two population means is given by

 

.

 

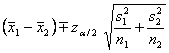Example 6.5 Consider a tire manufacturer who wishes to estimate the difference between the mean lives of two types of tires, Type A and Type B, as a prelude to a major advertising campaign. A sample of 100 tires is taken from each production process. The sample mean lifetimes are 30100 and 25200 miles, respectively whereas the sample variances are 1500000 and 2400000 miles squared, respectively.  Find a 99% confidence interval of the difference between the mean lives of the two types of tires.

 

Solution A 99% confidence interval for is given by

, i.e.

 

Confidence Interval for the Difference Between the Means of Two Independent Normal Populations, Variances Unknown but Equal

A % confidence interval (CI) for the difference in population means is given by

 

where  is the  percentile of student t distribution with degrees of freedom , and

.

 

Example 6.6 A random sample of 15 bulbs produced by an old machine was tested and found to have a mean life span of 40 hours with standard deviation 5 hours. Also, a random sample of 10 bulbs produced by a new machine was found to have a life span of 45 hours with standard deviation  hours. Assuming that the life span of a bulb has a normal distribution for both machines, and true variances are the same, construct a 95% confidence interval for the difference between the mean lives of the bulbs produced by two machines.

 

Solution  We have . The combined (pooled) estimate for the common variance is given by

 

.

 

With  degrees of freedom, , , a 95% confidence interval is given by

, i.e. .

 

Confidence Interval for the Difference Between the Means of Two  Independent Normal Populations, Variance Unknown and Equal Sample Sizes

If , a CI for  is given by the following approximate  t-interval:

 

where  has  2 (n – 1) degrees of freedom.

Example 6.7 A random sample of 16 bulbs produced by an old machine was tested and found to have a mean life span of 40 hours with standard deviation 5 hours. Also, a random sample of 16 bulbs produced by a new machine was found to have a mean life span of 45 hours with standard deviation  hours. Assume that the life span of a bulb has a normal distribution for both machines, construct a 99% confidence interval for the difference between the mean lives of the bulbs produced by two machines.

 

Solution We have . A 99% CI for is given by

, i.e.

                                                 

 

Confidence Interval for the Difference Between the Means of Two Independent Normal Populations, Neither the Variances nor the Sample Sizes Are Equal

ACI for  is given by the following approximate t-interval:

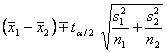
where  has the following degrees of freedom

 

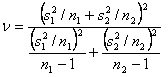
Example 6.8 A random sample of 12 bulbs produced by an old machine was tested and found to have a mean life span of 40 hours with variance 24 hours squared. Also, a random sample of 10 bulbs produced by a new machine was found to have a mean life span of 45 hours with variance 30 hours squared. Assume that the life span of a bulb has a normal distribution for both machines; construct a 95% confidence interval for the difference between the mean lives of the bulbs produced by the two machines.

 

Solution For old machine, we have  and for new machine, we have . The degrees of freedom is given by

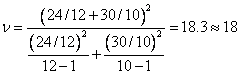
Since the degrees of freedom of here is 18,    and the required CI is

, i.e.

 

Matched-Pairs Samples

Letting i denote the th pair, with  and representing sample observations from the respective groups, we express the difference as and the mean of the differences by . The differences ’s are assumed to be independently and normally distributed. A  CI for is then given by

where  is the  percentile of student t distribution with  degree of freedom .

 

Example 6.9 (cf. Lapin, 1997, 329). The chief engineer in a machine parts manufacturing company is comparing Computer-Aided Design (A) to the traditional method (B). The two procedures are compared in terms of the mean time from start until production drawings and specifications are ready. A random sample of 10 parts has been selected, each to be designed twice, once by an engineer using borrowed time on the CAD (Computer-Aided Design) system at a nearby facility and again by an engineer in-house working in the traditional manner. The two engineers designing each sample part have been matched in terms of the quality of their past performance. The engineers in the CAD group have each just completed an after-hours training program and have been judged proficient in the new system. The following completion times (days) have been obtained:

 

Parts

1

2

3

4

5

6

7

8

9

10

CAD (X)

9.2

16.4

5.6

6.5

9.0

11.6

6.3

6.0

20.3

8.7

Traditional (Y)

12.5

26.2

5.0

7.0

12.5

10.4

9.1

7.4

21.1

10.3

 

Find a 95% confidence interval of the difference in mean time by CAD and by the traditional Method.

 

Solution

–3.3

–9.8

–0.6

–0.5

–3.5

1.2

–2.8

–1.4

–0.8

–1.6

 

A 95% CI for is then given by

.

 

6.5 Large Sample Confidence Interval Estimation of a Population Proportion

 

A confidence interval for is given by

.

 

Example 6.10 In certain water-quality studies, it is important to check for the presence or absence of various types of microorganisms. Suppose 20 out of 100 randomly selected samples of a fixed volume show the presence of a particular microorganism.  Estimate the true proportion of microorganism with a 90% confidence interval (Scheaffer and McClave, 1995, 369).

 

Solution Since the sample size is large, we use a z-interval. A 90% confidence interval for is given by

, i.e.

 

6.6         Large Sample Confidence Interval Estimation of the Difference Between Two Population Proportions

 

A confidence interval for is given by

 

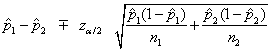
Example 6.11 We want to compare the proportion of defective bulbs turned out by two shifts of workers. From the large number of bulbs produced in a given week,  bulbs were selected from the output of Shift I, and  bulbs were selected from the output of Shift II. The sample from Shift I revealed four to be defective, and the sample from Shift II showed six faulty bulbs. Estimate, by a 95% confidence interval, the true difference between proportions of defective bulbs produced.

 

Solution Since the sample sizes are large, we use a z-interval. Here  and . With , a  95% CI  for is given by

, i.e. .

 

6.7 Confidence Interval Estimation of the Variance of a Normal Population

 

A  confidence interval for is given by

,

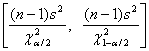where has  degree of freedom

 

Example 6.12 Consider the population of waiting times experienced by customers in Saudi Telecom Corporation.  Twenty five customers provide a standard deviation of 10.4 minutes. Find a 90% Confidence interval of the variance in waiting time for all similar waiting times.

 

 
Solution With 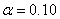, , 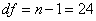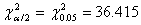and 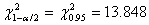 using Appendix A4,  90% CI for 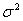is given by
 

.

 

i.e. .

 

Students are encouraged to find z, t and chi-square percentiles using Statistica.

 

 

 

 

Exercises

 

6.1        (cf. Walpole, R. E, et. al, 2002, 246).  The following measurements were recorded for the drying time, in hours, of a certain brand of latex paint:

 

3.4   

4.8   

2.8

3.3

4.0

4.4

5.2

5.6

4.3

5.6

 

Assuming that that the measurements represent a random sample from a normal population, find a 99% confidence interval of the true mean of drying time.

 

(a) Assume that population standard deviation is 1.3.

(b) Assume that population standard deviation is unknown.

 

6.2        (cf. Devore, J. L., 2000, 287). A random sample of fifteen heat pumps of a certain type yielded the following observations on lifetime (in years):

 

 

2.0

1.3

6.0

1.9

5.1

0.4

1.0

5.3

15.7

0.7

4.8

0.9

12.2

5.3

0.6

 

(a) Obtain a 95% confidence interval for expected (true average) lifetime.

(b) Obtain a 99% confidence interval for expected (true average) lifetime.

 

6.3        (cf. Devore, J. L., 2000, 299). Consider the following sample of fat content (in percentage) of  ten randomly selected hot dogs:

 

25.2

21.3

22.8

17.0

29.8

21.0

25.5

16.0

20.9

19.5

 

Assuming that these were selected from a normal population distribution, find a 95% C.I. for the population mean of fat content.

(a) Assume that population standard deviation is 2.4.

(b) Assume that population standard deviation is unknown.

 

6.4         (Devore, J. L., 2000, 303). A study of the ability of individuals to walk in a straight line  reported the accompanying data on cadence (stride per second) for a sample of  twenty randomly selected healthy men:

 

0.95

0.85

0.92

0.95

0.93

0.86

1.00

0.92

0.85

0.81

0.78

0.93

1.05

0.93

1.06

1.06

0.96

0.81

0.96

0.93

 

Calculate and interpret a 95% confidence interval for population mean cadence.

 

6.5         (Devore, J. L., 2000, 306). The following observations were made on fracture toughness of a base plate of 18% nickel steel:

 

69.5

71.9

72.6

73.1

73.3

73.5

75.5

75.7

75.8

76.1

76.2

76.2

77.0

77.9

78.1

79.6

79.7

79.9

80.1

82.2

83.7

93.7

 

Calculate a 99% CI for the actual mean of the fracture toughness.

 

6.6         (Devore, J. L., 2000, 307). For each of 18 preserved cores from oil-wet carbonate reservoirs, the amount of residual gas saturation after a solvent injection was measured at water flood-out. Observations, in percentage of pore volume, were:

 

23.5

31.5

34.0

46.7

45.6

32.5

41.4

37.2

42.5

46.9

51.5

36.4

44.5

35.7

33.5

39.3

22.0

51.2

 

Calculate a 98% CI for the true average amount of residual gas saturation.

 

6.7         (cf. Vining, G. G., 1998, 176). In a study of the thickness of metal wires produced in a chip-manufacturing process. Ideally, these wires should have a target thickness of 8 microns. These are the sample data:

 

8.4

8.0

7.8

8.0

7.9

7.7

8.0

7.9

8.2

7.9

8.1

7.8

8.2

7.9

8.2

7.9

7.8

7.9

7.9

8.0

8.0

7.6

8.2

8.1

8.3

7.8

8.0

8.0

8.3

7.8

8.2

8.3

8.0

8.0

7.8

8.2

7.7

7.8

8.3

7.8

7.9

8.4

7.7

8.0

7.9

8.0

7.7

7.7

7.8

8.3

8.0

7.5

 

Construct a 95% confidence interval for the true mean thickness.

 

6.8         (cf. Vining, G. G., 1998, 177). In a study of aluminum contamination in recycled PET plastic from a pilot plant operation at Rutgers University, they collected 26 samples and measured, in parts per million (ppm), the amount of aluminum contamination. The maximum acceptable level of aluminum contamination, on the average, is 220 ppm. The data are listed here:

 

291

222

125

  79

145

119

244

118

182

119

120

30

115

  63

  30

140

101

102

  87

183

  60

191

511

172

90

  90

 

Construct a 95% confidence interval for the true mean concentration.

 

6.9         (cf. Vining, G. G., 1998, 178). Researchers discuss the production of polyol, which is reached with isocynate in a foam molding process. Variations in the moisture content of polyol cause problems in controlling the reaction with isocynate. Production has set target moisture content of 2.125%. The following data represent 27 moisture analyses over a 4-month period.

 

2.29

2.22

1.94

1.90

2.15

2.02

2.15

2.09

2.18

2.00

2.06

2.02

2.15

2.17

2.17

1.90

1.72

1.75

2.12

2.06

2.00

1.98

1.98

2.02

2.14

2.10

2.05

 

Construct a 99% confidence interval for the true mean moisture content.

 

6.10  (cf. Vining, G. G., 1998, 178). In a study of a galvanized coating process for large pipes. Standards call for an average coating weight of 200 lb per pipe. These data are the coating weights for a   random sample of 30 pipes:

 

216

202

208

208

212

202

193

208

206

206

206

213

204

204

204

218

204

198

207

218

204

212

212

205

203

196

216

200

215

202

 

Construct 97%, 98% and 99% confidence intervals for the true mean coating weight.

6.11    (cf. Vining, G. G., 1998, 179). Researchers studied a batch operation at a chemical plant where an important quality characteristic was the product viscosity, which had a target value of 14.90. Production personnel use a viscosity measurement for each 12-hour batch to monitor this process. These are the viscosities for the past ten batches:

 

13.3

14.5

15.3

15.3

14.3

14.8

15.2

14.9

14.6

14.1

 

Construct a 90% confidence interval for the true mean viscosity.

 

6.12    (cf. Vining, G. G., 1998, 179). Scientists looked at the average particle size of a product with a specification of 70 – 130 microns and a target of 100 microns. Production personnel measure the particle size distribution using a set of screening sieves. They test one sample a day to monitor this process. The average particle sizes for the past 25 days are listed here:

 

  99.6

  92.1

103.8

  95.3

101.6

102.3

  93.8

102.7

  94.9

  94.9

102.8

100.9

100.5

102.7

  96.9

103.2

  97.5

  98.3

105.8

100.6

101.5

  96.7

  96.8

  97.8

104.7

 

 

 

 

 

 

Construct a 95% confidence interval for the true mean particle size assuming that true standard deviation is 5.2.

 

6.13    (cf. Vining, G. G., 1998, 184). In a study of cylinder boring process for an engine block. Specifications require that these bores be in. Management is concerned that the true proportion of cylinder bores outside the specifications is excessive. Current practice is willing to tolerate up to 10% outside the specifications. Out of a random sample of 165, 36 were outside the specifications. Construct a 99% confidence interval for the true proportion of bores outside the   specifications.

 

6.14  (cf. Vining, G. G., 1998, 184). Consider nonconforming brick from a brick manufacturing process. Typically, 5% of the brick produced is not suitable for all purposes. Management monitors this process by periodically collecting random samples and classifying the bricks as conforming or nonconforming. A recent sample of 214 bricks yielded 18 nonconforming. Construct a 98% confidence interval for the true proportion of nonconforming bricks.

 

6.15 (cf. Vining, G. G., 1998, 185). In a study examining a process for manufacturing electrical resistors that have a normal resistance of 100 ohms with a specification of ohms. Suppose management has expressed a concern that the true proportion of resistors with resistances outside the specifications has increased from the historical level of 10%. A random sample of 180 resistors yielded 46 with resistances outside the specifications. Construct a 95% confidence interval for the true proportion of resistors outside the specification.

 

6.16 (Vining, G. G., 1998, 185). An automobile manufacturer gives a 5-year/60,000-mile warranty on its drive train. Historically, 7% of this manufacturer's automobiles have required service under this warranty. Recently, a design team proposed an improvement that should extend the drive train's life. A random sample of 200 cars underwent 60,000 miles of road testing; the drive train failed for 12. Construct a 95% confidence interval for the true proportion of automobiles with drive trains that fail.

 

6.17 (Vining, G. G., 1998, 185). Historically, 10% of the homes in Florida have radon levels higher than recommended by the Environmental Protection Agency. Radon is a weakly radioactive gas known to contribute to health problems. A city in north central Florida has hired an environmental consulting group to determine whether it has a greater than normal problem with this gas. A random sample of 200 homes indicated that 25 had random levels exceeding EPA recommendations. Construct a 95% confidence interval for the true proportion of homes with excessive levels of radon.

 

6.18 (Devore, J. L., 2000, 382). Two types of fish attractors, one made from vitrified clay pipes and the other from cement blocks and brush, were used during 16 different time periods spanning 4 years at Lake Tohhopekaliga, Florida. The following observations are of fish caught per fishing day.

 

Pipe

6.64

7.89

0.42

0.85

0.29

0.57

0.63

1.83

0.32

0.37

0.00

0.11

4.86

1.80

0.23

0.58

Brush

9.73

8.21

2.17

0.75

1.61

0.75

0.83

0.56

0.76

0.32

0.48

0.52

5.38

2.33

0.91

0.79

 

Find a 95% confidence interval for the difference in means.

 

6.19 (Walpole, R. E, et al, 2002, 256).  Construct a 95% confidence interval for the difference in the mean stem weights between seedlings that receive no nitrogen and those that receive 368 ppm of nitrogen by using the following sample data. Assume the populations to be normally distributed.

 

Nitrogen

0.26

0.43

0.47

0.49

0.52

0.75

0.79

0.86

0.62

0.46

No nitrogen

0.32

0.53

0.28

0.37

0.47

0.43

0.36

0.42

0.38

0.43

 

6.20 (Walpole, R. E, et al, 2002, 254).  A study published in Chemosphere reported the levels of dioxin TCDD of 20 Massachusetts Vietnam veterans who were possibly exposed to Agent Orange. The amount of TCDD levels in plasma and in fat tissue is listed in the table below. Find a 95% confidence interval for the difference in means.

 

TCDD levels in plasma

2.5

3.1

2.1

3.5

3.1

1.8

  6.0

3.0

36.0

4.7

6.9

3.3

4.6

1.6

7.2

1.8

20.0

2.0

  2.5

4.1

TCDD levels in fat tissues

4.9

5.9

4.4

6.9

7.0

4.2

10.0

5.5

41.0

4.4

7.0

2.9

4.6

1.4

7.7

1.1

11.0

2.5

  2.3

2.5

 

6.21 (cf. Vining, G. G., 1998, 192). Researchers studied the impact of viscosity on the observed coating thickness produced by a paint operation. For simplicity, they chose to study only two viscosities: "low" and "high." Up to a certain paint viscosity, higher viscosities cause thicker coatings. The engineers do not know whether they have hit that limit or not. They thus wish to test whether the higher viscosity paint leads to thicker coatings. Here are the coating thicknesses:

 

Low Viscosity

1.09

1.12

0.83

0.88

1.62

1.49

1.48

1.59

1.65

1.71

0.88

1.29

1.04

1.31

1.83

1.76

 

 

 

 

High Viscosity

1.46

1.51

1.59

1.40

0.74

0.98

0.79

0.83

1.46

1.42

2.05

2.17

2.36

2.12

1.51

1.40

 

 

 

 

 

Construct a 95% confidence interval for the true difference in the mean coating thicknesses.

 

6.22 (Vining, G. G., 1998, 194). The following data are the yields for the last 8 hours of production from two ethanol-water distillation columns:

 

Column 1

70

74

73

72

72

73

72

73

Column 2

71

74

72

71

72

70

72

72

 

 Construct a 97 % confidence interval for the true difference in the mean yields.

 

6.23 (cf. Vining, G. G., 1998, p.192). A manufacturer of aircraft monitors the viscosity of primer paint. The viscosities for two different time periods are listed here:

 

Time Period I

33.8

33.1

34.0

33.8

33.5

34.0

33.7

35.2

33.8

33.3

33.5

33.2

33.6

33.0

33.5

33.1

 

 

 

 

Time Period II

33.5

33.3

33.4

33.3

34.7

34.8

34.8

33.2

35.0

35.0

34.8

34.5

34.7

34.3

34.6

34.5

 

 

 

 

 

Construct a 95% confidence interval for the true difference in the mean viscosities.

 

 

6.24 (cf. Vining, G. G., 1998, 193). An independent consumer group tested radial tires from two major brands to determine whether there were any differences in the expected tread life. The data (in thousands of miles) are given here:

 

Brand 1

50

54

52

47

61

56

51

51

48

56

53

43

58

52

48

Brand 2

57

61

47

52

53

57

56

53

67

58

62

56

56

62

57

 

Construct a 95% confidence interval for the true difference in the mean tread lives.

 

6.25 (cf. Vining, G. G., 1998, 194). In a comparison of two brands of ultrasonic humidifiers with respect to the rate at which they output moisture, the following data are the maximum outputs (in fluid ounces) per hour as measured in a chamber controlled at a temperature of F and a relative humidity of 30%:

 

Brand 1

14.0

14.3

12.2

15.1

Brand 2

12.1

13.6

11.9

11.2

 

Construct a 90% confidence interval for the true difference in the mean viscosities.