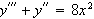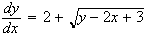1. Given the system
   
   

   1. (3pts) Change the system into a system of first order linear differential equations;

   2. (7pts) using part (a) or any other method, find the solution of the system that satisfies

2. Given the system
   
   

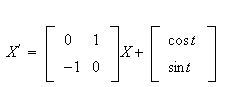
   1. (4pts) Find the General solution of the system.

   2. (2pts) Find a solution of the system satisfying

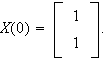
   3. (4pts) Find the value of 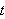for which Also find 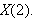Simplify.

3. For the differential equation
   
   

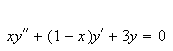
   1. (2pts) Find the indicial equation and the indicial roots.

   2. (6pts) Use Frobenius method to show this equation has a polynomial solution such that the leading coefficient is 1.

   3. (2pts) Find the second linearly independent solution.

4.  

   1. (5pts) A thermometer is taken from a room where the air temperature is 70F to the outside where the temperature reads 10F. After 1/2 minute the thermometer reads 50F What is the reading at 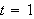minute? How long will it take for the thermometer to read 15F?.

   2. (3pts) Find a second order differential equation whose roots are

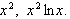
5. (8pts ea.) Find the general solution (when applicable) of the differential equations

   1. 

   2. 

   3. 

   4. 

   5. 

Back