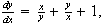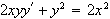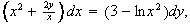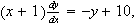(3pts) Verify that
is a solution of the differential
equation
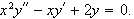
(5pts ea.) Solve the following differential equations
(8pts) A large tank is partially filled with 100 gallons of
fluid in which 10 pounds of salt is dissolved. Brine containing
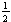pounds of salt per gallon is pumped into the tank at a rate of 6 gallons per
minute.. The well mixed solution is then pumped out at a slower rate of 4
gallons per minute.. Find the number of pounds of salt in the tank after 3
minutes. If the capacity of the tank is 400 gallons, find the number of pounds
of salt in the tank just as it overflows.
(4pts) Given that
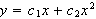is a two parameter family of solutions of
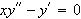on the interval
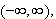can you find a solution of the differential equation satisfying the initial
conditions
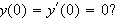Is the solution unique? Do your answers contradict the existence and
uniqueness theorem? Explain.