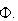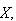

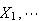 etc and
etc and





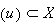 is an open neighbourhood of
is an open neighbourhood of

In this section

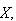

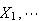 etc and
etc and

![]() are Banach spaces over
are Banach spaces over



![]()

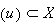 is an open neighbourhood of
is an open neighbourhood of

![]() .
.
An operator
![]()
is
called

 -linear
and bounded if it is linear in each of its arguments and there exists a
-linear
and bounded if it is linear in each of its arguments and there exists a

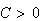 such
that
such
that
![]()
The
norm of

![]() is defined
by
is defined
by

Then
![]()
Every

 -linear
bounded operator is continuous.
-linear
bounded operator is continuous.
In the sequel we will write

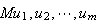 for
for

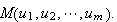
Suppose

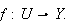
The differential of

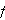 at
at

![]() exists if there exists a bounded linear operator
exists if there exists a bounded linear operator

 such that
such that
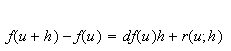
with
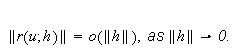
The second differential of

 at
at

![]() exists if there exists a bounded bilinear operator
exists if there exists a bounded bilinear operator

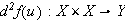 such
that
such
that
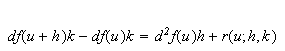
with

Inductively we define
The

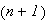 th
differential of
th
differential of

 at
at

![]() exists if there exists a bounded
exists if there exists a bounded

 -linear
operator
-linear
operator

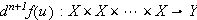 such
that
such
that
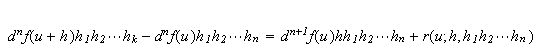
with
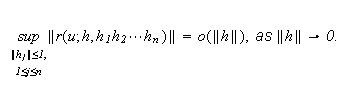
The differentials

 are also dentoed by
are also dentoed by

 We also write
We also write

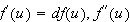 =
=
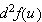 and so on. The diferentials
and so on. The diferentials

 are called the Frechet derivatives of
are called the Frechet derivatives of

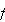 at
at

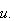 To formally find the Frechet derivatives we use the
formula
To formally find the Frechet derivatives we use the
formula
![]()
Once
we have a formula for the derivative we proceed to prove that it is the
desired one. This involves establishing two things:
the resulting operator is multilinear,bounded, and
the remainder is

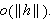

 is continuous at
is continuous at

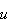 if for each
if for each

 there exists a
there exists a

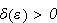 such that
such that
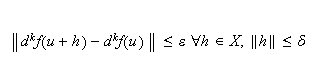
This means that for all

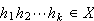 and all
and all

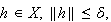
![]()



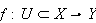 is called a
is called a

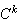 function if
function if

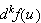 is continuous on
is continuous on

If

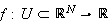 has continuous paritial derivatives of order
has continuous paritial derivatives of order

 then
then

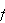 is
is

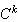 and
and
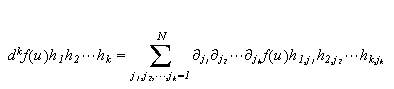
where

(
 )
write
)
write

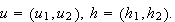 Then
Then

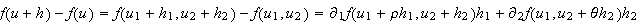 for some
for some

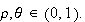 Hence,
Hence,

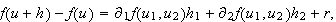 where
where

so
that
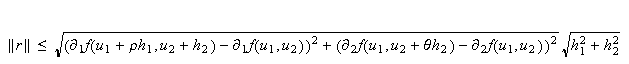
and
the continuity of the partial derivatives give that

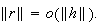
(Bilinear Operators)
Suppose

 is a bilinear bounded operator. Then
is a bilinear bounded operator. Then

 is
is

Set

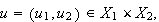

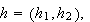

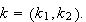 Let's illustrate first the formal calculation of
Let's illustrate first the formal calculation of

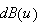 and
and


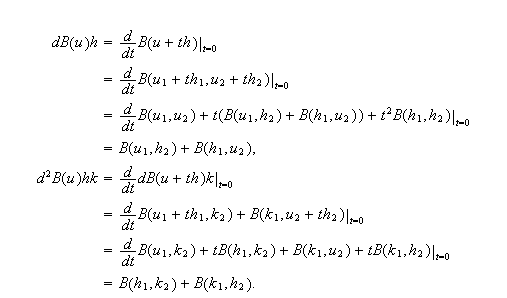
Next,
we verify that these are the required derivatives. We begin with

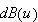

![]() Then
Then

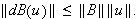 i.e.,
i.e.,

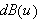 is a bounded linear operator on
is a bounded linear operator on

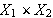 into
into

 .
.

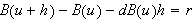 where
where

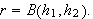 Hence,
Hence,

![]()
Similarly, for

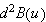 we have:
we have:

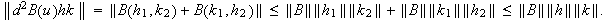 Then
Then

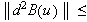

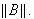 i.e.,
i.e.,

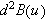 is a bounded bilinear operator on
is a bounded bilinear operator on

![]() into
into

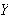 .
.

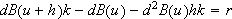 where
where

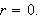
Next we establish the continuity of

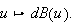
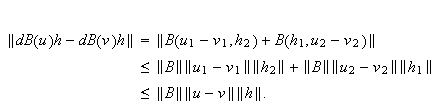
Hence,

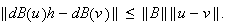 i.e.,
i.e.,

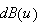 is actually Lipschitz continuous. The continuity of
is actually Lipschitz continuous. The continuity of

 is easier to see since it is independent of
is easier to see since it is independent of

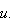 Finally,
Finally,

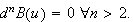
Suppose

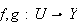 have Frechet derivatives of order
have Frechet derivatives of order

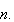 Then
Then
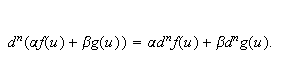
Suppose

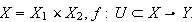 Let
Let

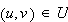 and define the function
and define the function

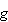 by
by
![]()
If

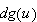 exists, we define the partial Frechet derivative
exists, we define the partial Frechet derivative

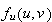 of
of

 at
at

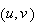 by
by
![]()
The
partial derivative

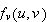 of
of

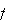 at
at

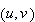 is defined in a similar manner. Partial derivatives are also denoted by
is defined in a similar manner. Partial derivatives are also denoted by

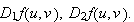
If

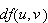 exists then
exists then

 and
and

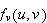 both exist and
both exist and
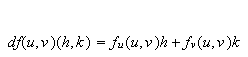
With the above definition of

 we
have
we
have
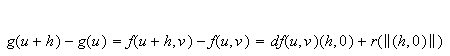
where

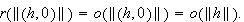 i.e.,
i.e.,

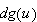 exists and
exists and

 Hence,
Hence,
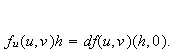
Similarly,
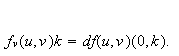
Using
the linearity of

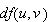 we obtain the assertion of the proposition.
we obtain the assertion of the proposition.
Let

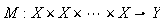 be a
be a

![]() -linear
bounded operator which is symmetric with respect ot all its arguments. This
means that
-linear
bounded operator which is symmetric with respect ot all its arguments. This
means that

![]() is invariant under any permutation of its argument. A power operator generated
by
is invariant under any permutation of its argument. A power operator generated
by

![]() is defined
by
is defined
by
![]()
and
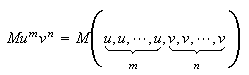
where



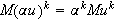

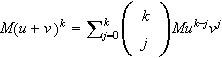
(e.g., for

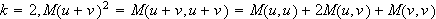 since
since

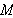 is symmetric.)
is symmetric.)

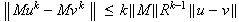 when
when

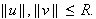
To see this, we write
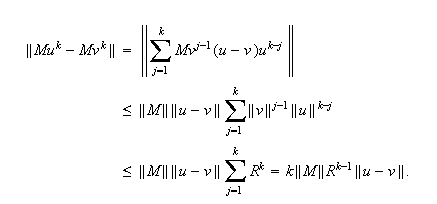

 has Lipschitz continuous derivatives of all orders
and
has Lipschitz continuous derivatives of all orders
and
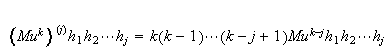
For
example, when

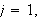

where

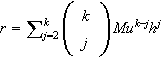 with
with
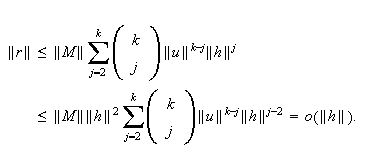
Also,

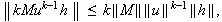 which shows the continuity of the operator
which shows the continuity of the operator

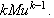 Hence,
Hence,

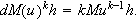 The Lipschitz continuity of
The Lipschitz continuity of

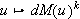 can be shown as
follows:
can be shown as
follows:
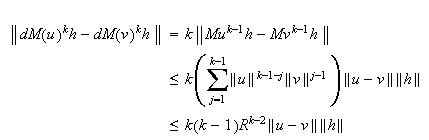
for

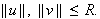
Suppose

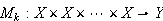 is a power operator for
is a power operator for

 Furthermore, suppose that the
series
Furthermore, suppose that the
series
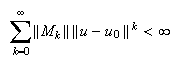
for
all

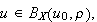

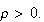 The operator
The operator

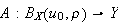 defined by
defined by
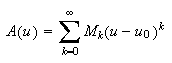
is
called a power series. Note that () gurantees that

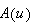 is a well defined element of
is a well defined element of

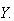
An operator

 is called analytic at the point
is called analytic at the point

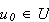 if there exists a
if there exists a

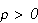 such that
such that

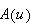 admits a power series representation () that is absolutely convergent (i.e.,
() converges) for every
admits a power series representation () that is absolutely convergent (i.e.,
() converges) for every

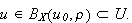
If

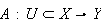 is analytic at the point
is analytic at the point

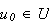 then
then

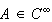 on
on

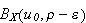 for any
for any

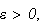 where
where

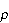 is as in Definition . Moreover,
is as in Definition . Moreover,

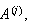



 can be found by term by term differentiation of ().
can be found by term by term differentiation of ().
We will show that
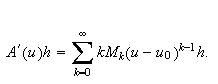
For
this we
have
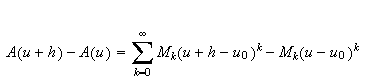
and

where

Now,
for

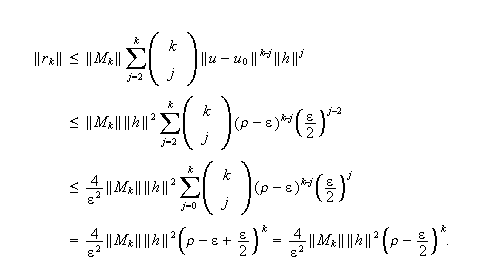
Furthermore,

where

![]() Since
Since

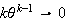 as
as

![]() then
then

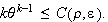 Hence,
Hence,
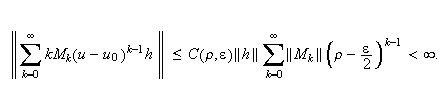
Therefore,
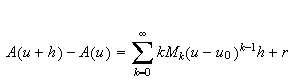
where

![]() It remains to show that
It remains to show that

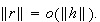 This follows
from
This follows
from
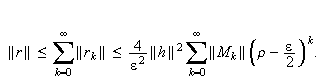
The
statement about higher derivatives can be shown in the same manner.
Suppose

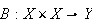 is a bounded bilinear operator,
is a bounded bilinear operator,

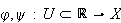 such that
such that

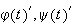 exist at some point
exist at some point

 Then
Then

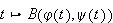 is differentiable
and
is differentiable
and
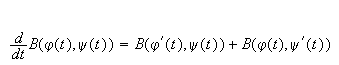

where

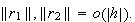 Hence,
Hence,
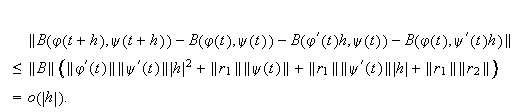
Denote the subset of

 of operators with bounded inverse by
of operators with bounded inverse by

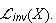 Define
Define
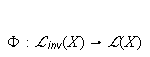
by
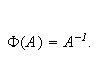
Then

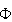 is analytic at
is analytic at

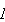 ,
and
,
and
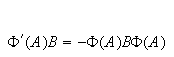
for
all

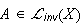 and all
and all

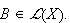
For

 let
let

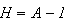 .
Then
.
Then
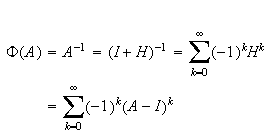
Since
the
series
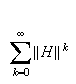
converges, it follows that the series for

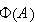 is absolutely convergent. Hence
is absolutely convergent. Hence

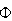 is analytic at
is analytic at

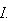 To find
To find

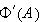 we use the formal
calculation
we use the formal
calculation
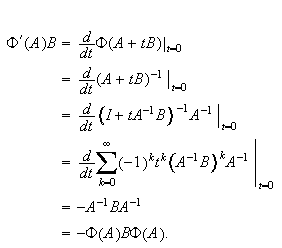
Now
noting that

![]() is a bilinear operator, we use formula to compute higher derivatives of
is a bilinear operator, we use formula to compute higher derivatives of

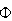 .
For the second derivative we
get
.
For the second derivative we
get
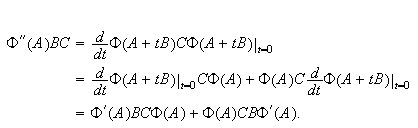
This
formula can, in turn, be used to obtain higher derivatives of