MATLAB Function

ode45:

Solve initial value problems for ordinary differential equations (ODEs)

Example 1.

An example of a system is the system of differential equations describing the motion of a rigid body without external forces.

1- we create a function rigid containing the equations
	function dy = rigid(t,y) dy = zeros(3,1); % a column vector dy(1) = y(2) * y(3); dy(2) = -y(1) * y(3); dy(3) = -0.51 * y(1) * y(2);
2- we write this command to solve the problem
	[t,y] = ode45('rigid',[0 12],[0 1 1]);
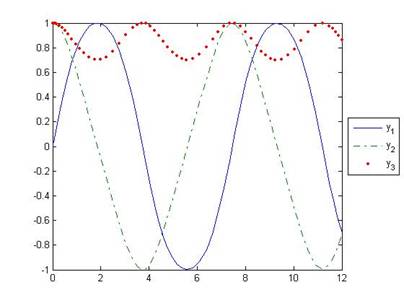
3- we write these commands to plot the graph
	plot(t,y(:,1),'-',t,y(:,2),'-.',t,y(:,3),'.') legend('y_1','y_2','y_3','Location','eastoutside');
4- we write this command to see the values
	[t,y]
		t y1 y2 y3 0 0 1.0000 1.0000 0.0001 0.0001 1.0000 1.0000 0.0001 0.0001 1.0000 1.0000 0.0002 0.0002 1.0000 1.0000 0.0002 0.0002 1.0000 1.0000 0.0005 0.0005 1.0000 1.0000 0.0007 0.0007 1.0000 1.0000 0.0010 0.0010 1.0000 1.0000 0.0012 0.0012 1.0000 1.0000 0.0025 0.0025 1.0000 1.0000 0.0037 0.0037 1.0000 1.0000 0.0050 0.0050 1.0000 1.0000 0.0062 0.0062 1.0000 1.0000 0.0125 0.0125 0.9999 1.0000 0.0188 0.0188 0.9998 0.9999 0.0251 0.0251 0.9997 0.9998 0.0313 0.0313 0.9995 0.9997 0.0627 0.0627 0.9980 0.9990 0.0941 0.0939 0.9956 0.9977 0.1255 0.1250 0.9922 0.9960 0.1569 0.1560 0.9878 0.9938 0.2760 0.2709 0.9626 0.9811 0.3951 0.3803 0.9249 0.9624 0.5143 0.4824 0.8760 0.9388 0.6334 0.5758 0.8176 0.9115 0.7975 0.6888 0.7249 0.8707 0.9616 0.7829 0.6222 0.8291 1.1257 0.8583 0.5129 0.7900 1.2898 0.9162 0.4002 0.7560 1.5240 0.9713 0.2371 0.7201 1.7582 0.9971 0.0731 0.7019 1.9924 0.9956 -0.0909 0.7030 2.2267 0.9666 -0.2546 0.7232 2.5015 0.8954 -0.4458 0.7691 2.7764 0.7764 -0.6300 0.8322 3.0513 0.6052 -0.7953 0.9014 3.3262 0.3838 -0.9231 0.9616 3.5080 0.2146 -0.9764 0.9880 3.6898 0.0355 -0.9992 0.9996 3.8717 -0.1451 -0.9894 0.9947 4.0535 -0.3191 -0.9478 0.9739 4.2353 -0.4785 -0.8782 0.9400 4.4172 -0.6180 -0.7864 0.8976 4.5990 -0.7347 -0.6784 0.8515 4.7808 -0.8280 -0.5602 0.8063 4.9737 -0.9030 -0.4290 0.7642 5.1666 -0.9552 -0.2949 0.7311 5.3594 -0.9868 -0.1600 0.7093 5.5523 -0.9992 -0.0250 0.7003 5.8266 -0.9857 0.1667 0.7101 6.1008 -0.9331 0.3584 0.7454 6.3750 -0.8367 0.5467 0.8016 6.6493 -0.6911 0.7223 0.8696 6.8774 -0.5294 0.8482 0.9258 7.1056 -0.3351 0.9421 0.9710 7.3338 -0.1175 0.9929 0.9964 7.5619 0.1096 0.9939 0.9969 7.7901 0.3287 0.9443 0.9719 8.0182 0.5244 0.8517 0.9273 8.2464 0.6871 0.7269 0.8717 8.4745 0.8132 0.5817 0.8142 8.6643 0.8912 0.4534 0.7715 8.8541 0.9467 0.3217 0.7370 9.0439 0.9817 0.1889 0.7131 9.2337 0.9981 0.0561 0.7014 9.5047 0.9909 -0.1335 0.7066 9.7758 0.9459 -0.3232 0.7373 10.0468 0.8594 -0.5105 0.7894 10.3179 0.7257 -0.6876 0.8552 10.6096 0.5228 -0.8524 0.9281 10.9013 0.2695 -0.9631 0.9815 11.1930 -0.0118 -0.9990 0.9992 11.4847 -0.2936 -0.9540 0.9763 11.6136 -0.4098 -0.9102 0.9548 11.7424 -0.5169 -0.8539 0.9279 11.8712 -0.6135 -0.7874 0.8974 12.0000 -0.6987 -0.7128 0.8650
All above commands can be invoked by using the following two files math202.m and rigid.m