In other words the genearl solution of eqn (5) is the
linear combination of
n linearly independent solutions.
on an open interval I where the functions pi
(x) are continuous. Then, every solution of eqn (5)
can be written as a linear combination of these solutions.
That is, if y(x) is a solution then there are constants
c1, c2, ....., cn such that
y(x) = c1
y1(x) + c2 y2
(x) + ..........+ cn
yn
(x) for all x in I
Theorem: The general soltuion of Homogeneous
Equations:
Let y1, y2, ...., y
n
be n linearly independent solutions of the the nth
order homogenous equation
Theorem3:
(The wronskian of solutions)
See the text.
Definition: (The
wronskian)
See the text.
Definition: (Hard
to apply)
Two functions are linear indep if one is not a scalar
multiple of the of the other.
Linearly independent
functions
------------------------------------------------------------
This does not contradicts the theorem since dividing
by x2
makes the coefficients of y` and y non continuous
functions at x = 0 (where the initial values are specified.)
are two solutions of the IVP
has a unique solution on the entire interval I.
y(n) + pn-1 y
(n-1) + ......+ p1
y' + p0 y =
f(x)
y(a) = b0
y1(a) = b2
y(n-1)
(a) = bn-1
Existence and Uniqueness of solution to the IVP
Suppose the p0(x),
p1(x), ,
pn-1
are cont on the open interval I containing the point
a. The the IVP
for some constants c1,c
2, and c3.
So the wronskian in never zero for all x. Therefore,
solutions are linearly independent and the general
solution is given by
Compute
the
derivatives
of
the
solutions
Example
The function
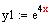
,

and
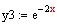
are three solutions of the diff eqn
y(3)
- 6 y'' +32 y =0 .
The wornskian of these solutions is
Example
Verify, by substation, that the two functions
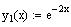
and
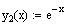
are solutions to the differential equation y'' +
3y' + 2y =0
Note:
1. The principle of superposition is simply stating
that a constant multiple of any solution is also a
solution.
2. The sum of any number of solutions is also a solution.
3. The principle applies to homogenous
linear diff eqns only.
The principle of superposition:
Let y1, y2, .., yn
be n solutions of the
homogeneous eqn (3) on an interval I, then the linear combination:
y = c1
y1 +..
+ cn
yn
(for some constants c1, c2
, ...,cn
)
is also a solution on I.
Equation 2 is called the standard
form
of a nonhomogenous nth order linear differential equation.
The associated
homogeneous linear differential equation is given
by
then we can rewrite equation (1) as
Note:
1.

denotes the nth derivative of y, that is
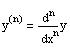
2. Linearity is assured by requiring that the coefficient
of the unknown function y and its derivatives be functions
of x (and x alone).
3. The function F(x) is called the nonhomogenous term.
4. If F(x) = 0 then the differential equation is called
the associated
homogenous
differential equation.
The general nonhomogenous
nth order linear differential equation has the form
The material of section 5.1 is limited to the 2nd order
linear differential equations. The same topics are
repeated in section 5.2 of the nth order linear differential
equation. Thus, section 5.1 is a special case of section
5.2.
5.1-2-3 Higher Order Linear
Diff Equations
Thus, the linear combination of the two solutions is
also a solution.
Note:
Mathcad is used to substitute the above values into
the left-hand side of the diff eqn and it returned
0, which equals the right-hand side of the equation.
(Substitute y and its derivatives into the differential
equation.
(compute the 2nd deriv. of the first soln)
(Compute the first deriv. of the first soln)
(Define y as a lin. comb. of the two solns)
Similarly, if
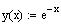
, then (using mathcad to substitute in the eqn)
(substitute in the diff eqn)
(compute the 2nd deriv. of the first soln)
(Compute the first deriv. of the first soln)
(set y(x) equal the first son)