Topological Sorting
Objectives of this lecture
q Learn two algorithms for traversing a directed graph
What is Topological Sorting?
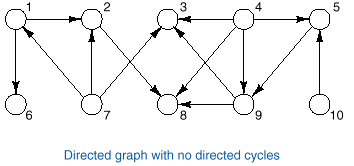
q If G is a directed graph with no
directed cycles, then a topological order for G is a
sequential listing of all the vertices in G such that, for all
vertices v, w in G, if there is an edge from v to w, then v precedes w in the sequential
listing
q Notice that Topological sorting is only applicable to directed acyclic graph --one with no
directed cycles.
q An example of problem requiring topological ordering
is ordering of courses where an edge is defined from one course A, to another course, B if A is a prerequisite for B
q Another example is a listing of technical terms such
that no term is used in a definition before it is, itself, defined.
q Two different topological orders of directed graph are
shown in the following figures.
Implementation of topological ordering
q As an example of graph traversal implementation, we
shall implement the two topological ordering for a graph G implemented using mix representation.
q The function will produce an array
Vertex toporder[MAXVERTEX];
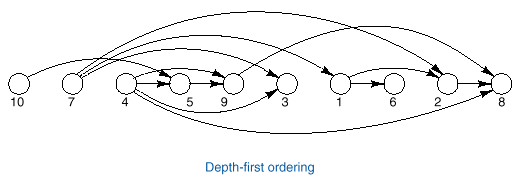
Depth-First
Algorithm.
q Topological order requires that a vertex must appear
before all its successor.
q Thus, in this approach, when we take a vertex, we must
process all its successors recursively before we can place it in its correct
place.
q Thus, the
first vertex to be placed is the last in the array toporder (one with no successor).
q The following function implements the algorithm.
/* DepthTopSort: generate depth-first topological orderingPre: G is a directed graph with no cycles implemented with a contiguous list of vertices and linked adjacency lists.Post: The function makes a depth-first traversal of G and generates the resulting topological order in the array T.Uses: RecDepthSort performs the recursive depth-first traversal. */void DepthTopSort(Graph *G, Toporder T){ Vertex v; /* next vertex whose successors are to be ordered */ int place; /* next position in the topological order to be filled */ for (v = 0; v < G->n; v++) visited[v] = FALSE; place = G->n - 1; for (v = 0; v < G->n; v++) if (!visited[v]) RecDepthSort(G, v, &place, T);} /* RecDepthSort: perform recursion for DepthTopSort.Pre: v is a vertex of the graph G and place is the next location in the topological order T to be determined (starting from the end of the final ordered list).Post: The procedure puts all the successors of/ v and finally/ v itself into the topological order T in depth-first order.Uses: Global array visited and RecDepthSort recursively. */void RecDepthSort(Graph *G, int v, int *place, Toporder T){ Vertex curvertex; /* vertex adjacent to v */ Edge *curedge; /* traverses list of vertices adjacent to v */ visited[v] = TRUE; curedge = G->firstedge[v]; // Find the first vertex succeeding v. while (curedge) { curvertex = curedge->endpoint; //curvertex is adjacent to v. if (!visited[curvertex]) RecDepthSort(G, curvertex, place, T); //Order the successors curedge = curedge->nextedge; // Go on to the next immediate } T[*place] = v; /* Put v itself into the topological order. */ (*place)--;}
Analysis:
q Notice that this algorithm visit each node exactly
once and follow each edge once. Its
running time is therefore O(n+e), where n is the number of vertices and e is
the number of edges.
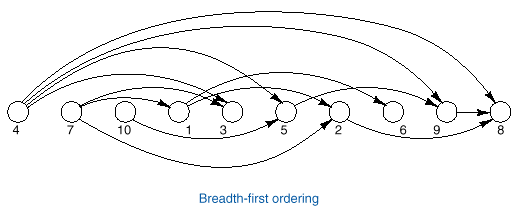
Breadth-First
q In this method, we use an integer array predecessorcount that stores the number of predecessors of each
vertex.
q We first place those vertices with zero predecessors
in a queue
q We then repeat the following while the queue is not
empty
Ø
Remove and visit (place
in the ordered array) the next vertex, v, from the queue
Ø
subtract 1 from the
number of predecessors of each successor of v
Ø
If the number of predecessors
of any successor of v reduces to zero after subtracting 1, place it in the queue
q The following diagram illustrates this method.
q The function below implements the method.
/* BreadthTopSort: generate breadth-first topological orderingPre: G is a directed graph with no cycles implemented with a contiguous list of vertices and linked adjacency lists.Post: The function makes a breadth-first traversal of G and generates the resulting topological order in T.Uses: Functions for processing queues. */void BreadthTopSort(Graph *G, Toporder T){ int predecessorcount[MAXVERTEX]; Queue Q; /* vertices ready to be placed into the order */ Vertex v; /* vertex currently being visited */ Vertex succ; /* one of the immediate successors of v */ Edge *curedge; /* traverses the adjacency list of v */ int place; /* next position in topological order */ /* Initialize all the predecessor counts to 0. */ for (v = 0; v < G->n; v++) predecessorcount[v] = 0; /* Increase the predecessor count for each vertex that is a successor. */ for (v = 0; v < G->n; v++) for (curedge = G->firstedge[v]; curedge; curedge = curedge->nextedge) predecessorcount[curedge->endpoint]++; CreateQueue(&Q); /* Place all vertices with no predecessors into the queue. */ for (v = 0; v < G->n; v++) if (predecessorcount[v] == 0) Append(v, &Q); /* Start the breadth-first traversal. */ place = -1; while (!QueueEmpty(Q)) { /* Visit v by placing it into the topological order. */ Serve(&v, &Q); place++; T[place] = v; /* Traverse the list of immediate successors of v. */ for (curedge = G->firstedge[v]; curedge; curedge = curedge->nextedge) { // Reduce the predecessor count for each immediate successor succ = curedge->endpoint; predecessorcount[succ]--; if (predecessorcount[succ] == 0) // succ has no further predecessors, so it is ready to process. Append(succ, &Q); } }}
Analysis:
q As with depth-first, the time required by the
breath-first function is also O(n+e).