Binary Search Trees (BST)
Objectives of this lecture
q Learn about Binary Search
Trees – how it solves the draw-backs of linked list
q Study the operations of BST,
TreeSearch, InsertTree, TreeSort, and DeleteNode.
What is Binary Search Tree?
q Binary search tree is
another important type of binary tree that is used in information retrieval
applications.
q A binary search tree is
defined as a binary tree that is either empty or in which every node contains a
key such that:
Ø The keys in the left subtree
(if it exists) are less than the key in the root
Ø The keys in the right
subtree (if it exists) are greater than the key in the root
Ø The left and right subtrees
(if they exists) are again binary search trees
q Note the above definition
can be modified to allow for duplicate keys.
q Notice also that in BST,
there must be a key as part of the entry. Thus we shall assume that TreeEntry has the following
declaration.
typedef
… KeyType;
typedef
struct {KeyType key;
……
} TreeEntry;
q We can apply the operations
already defined for general binary trees to BST without difficulty. these includes: CrateTree, ClearTree, TreeEmpty, TreeFull and the three traversal functions.
Further operations on Binary Search Trees
TreeSearch:
q The first important additional
operation for BST is the Search operation.
q To search for a target, we
first compare it with the key of the root.
If it is the same, we are done.
If it is not the same, we go to the left subtree or to the right subtree
as appropriate and repaeat the process.
This continue until we either find the target or we reach a subtree that
is empty.
/*
TreeSearch: search for target starting at node root.
Pre: The tree to which root points has been
created.
Post:
It returns a pointer to a tree node that matches target
or
NULL if the target is not in the tree.
*/
TreeNode
*TreeSearch(TreeNode *root, KeyType target)
{
if (root)
if (LT(target, root->entry.key))
root = TreeSearch(root->left, target);
else if (GT(target,
root->entry.key))
root = TreeSearch(root->right,
target);
return root;
}
Analysis
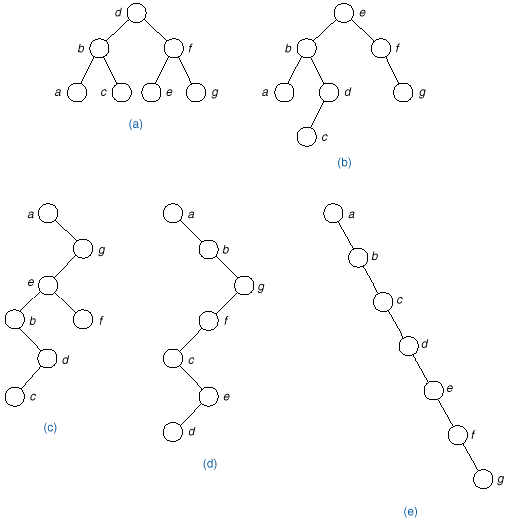
q If we apply binary search to an ordered (contiguous)
list and draw its comparison tree (figure (a) below), we can see that TreeSearch does the same number of
comparisons when applied to this same tree.
Thus, for a well (or nearly) balanced BST, the performance of TreeSeach
is the same (or about the same) as BinarySearch. i.e O(log n).
q
q
q
q However, since, the
representation of binary tree is not unique (see other possible representations
(b) –
(e)
above), it cannot be guaranteed that TreeSearch will always give O(log n) performance.
q Nevertheless, in practice,
if the keys are built into a binary search tree in random order, it is very
unlikely that it will degenerate as badly as in fig (d) and (e) above.
Insertion into a binary search tree
q The next important operation
is the insertion of a new node into a binary search tree. It must be done such that the keys remain in
order.
q To insert a node into an
empty tree, we only need to make it the root and set its left and right
subtrees to be NULL.
q To insert into a non-empty
tree, we must compare the key with the one on the root. If it is less, we insert on the left
subtree. If it is more, we insert on
the right subtree. If it is equal, we
adopt the convention of inserting the duplicate key into the right subtree.
/*
InsertTree: insert a new node in the tree.
Pre: The binary search tree to which root points
has been created.
The parameter newnode points to a node
that has been created and
contains a key in its entry.
Post:
The node newnode has been inserted into the tree in such a way
that the properties of a binary search
tree are preserved.
*/
TreeNode
*InsertTree(TreeNode *root, TreeNode *newnode)
{
if (!root) {
root = newnode;
root->left = root->right = NULL;
} else if (LT(newnode->entry.key,
root->entry.key))
root->left =
InsertTree(root->left, newnode);
else
root->right =
InsertTree(root->right, newnode);
return root;
}
q The following figure shows
what happens when we insert the keys: e, b, d, f, a, g, c into an initially empty tree in the order given.
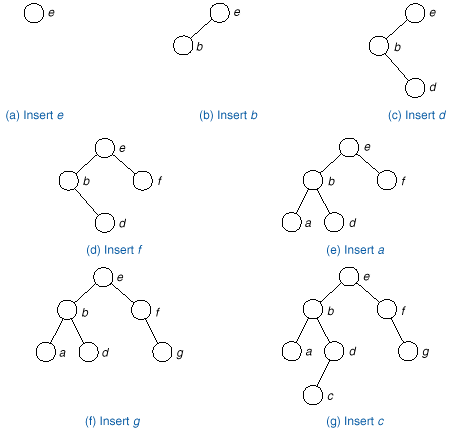
q Note that it is quite
possible that a different order of insertion can produce the same binary
tree. For example the following:
e, f, g, b, a, d, c or e, b, d,
c, a, f, g.
TreeSort:
q Observe that another sorting
method, called TreeSort, can be obtained by inserting a list of elements into a binary search
tree and then using Inorder traversal to output them.
q One advantage of this
sorting method is that the elements need not all be available at the start of
the process, but are built into the tree as they become available. Hence TreeSort can be very useful in
applications where elements are recorded one at a time.
q The performance of TreeSort
on a ramdomly ordered list is O(n log n).
q However, it is suffers from
the same draw-back as QuickSort since for a degenerate tree, the performance can be
n2.
Deletion from a binary tree:
q There are three cases to
consider when deleting a node from a binary search tree.
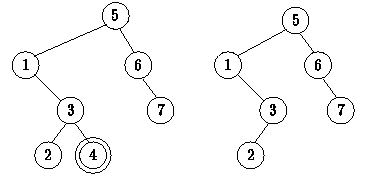
q If the node to be deleted is
a leaf
node, then the deletion is easy; we need only to replace the link to the
deleted node by NULL as shown by the following figure:
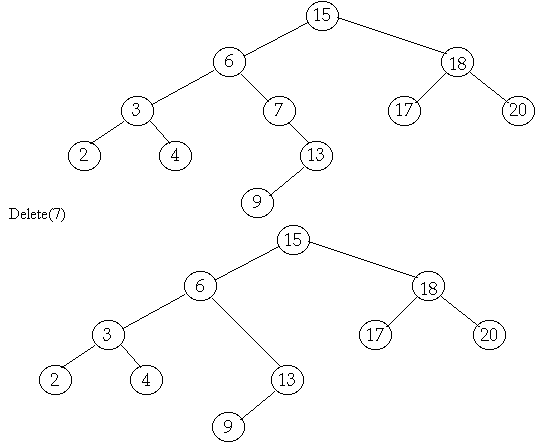
q If the node to be deleted
has only one subtree, again the deletion is easy, we need only to link the parent of the
node to its (only one) child as shown in the figure below:
q If the node to be deleted
has two children, then the operation is a bit complicated –how do we link the two
hanging subtrees?. There are two
methods.
Method 1:
q The right subtree is linked
with the parent of the deleted node. If
no such parent exists (i.e the root is being deleted), the right child becomes
the root.
q The left subtree is linked
with the smallest element of the right subtree. The smallest element of the right subtree is obtained by
traversing to the left of the right child until NULL is reached. The following
figure illustrates this.
q
q 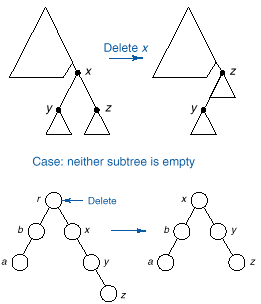
q
q The following code
implements these ideas.
/*
DeleteNodeTree: delete a new node from the tree.
Pre: The parameter p is the address of a node in
a binary search
tree, and p
is not NULL.
Post:
The node p has been deleted from the binary search tree and
the
resulting tree has the properties of a binary search tree.
*/
void
DeleteNodeTree(TreeNode **p)
{ TreeNode *r = *p, *q; /* used to find place for left subtree */
if (r == NULL)
Error("Attempt to delete a
nonexistent node ");
else if (r->right == NULL) {
*p = r->left; /* Reattach left subtree. */
free(r); /* Release node space. */
} else if (r->left == NULL) {
*p = r->right; /* Reattach right subtree. */
free(r);
} else { /* Neither subtree is empty. */
for (q = r->right; q->left; q =
q->left); //inorder successor
q->left = r->left; /* Reattach left subtree. */
*p = r->right; /* Reattach right subtree. */
free(r);
}
}
q Note that since most of the
times, we only have the key of the node to be deleted, before we can use the
above function, we must use the TreeSearch Function to find its address.
q The problem with method 1 is
that it could make the height of the resulting tree higher that it was before
deletion as shown by the following:
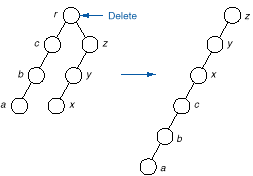
Method 2:
q To delete a node d, with two children, we
first find the node with the next higher (or lower) key. We then swap this node with d and then delete d. This ensures that the
height of the resulting tree is not higher than the original tree.
q To find the node with next
higher key (also called inorder successor), we traverse to the left of d’s right child until we
reach NULL.
q To find the node with next
lower key (also called inorder predecessor), we traverse to the right of d’s left child until we reach
NULL
q The following figure
illustrates this method but its implementation is left as exercise.
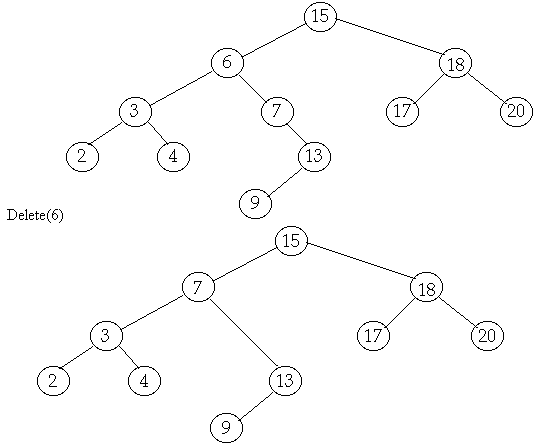
Exercises:
Implement
DeleteNode function using method 2.
Try Exercises E1-E5, of
pages 409-410 of your book.