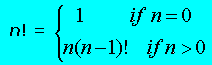Review of Recursion
Objectives of this lecture
q Review how recursive functions works, their good and
bad points
q Study some examples of recursive functions.
Review
q We recall that a recursive function is one that call
itself, or start call chain that eventually calls itself.
q It is based of the divide and conquer problem-solving
approach.
q It is a very powerful tool for simplifying algorithms
q However, it can also be very expensive in terms of
memory requirement
q A recursive function generally consists of two parts:
The recursive part, in which the function calls itself, and the stopping part
(also called the base case) which stops the recursion.
Example 1:
q The most popular example of recursion in the
implementation of factorial function, which is defined mathematically as:
q The implementation is almost a direct representation
of this definition
/*
Factorial: compute n!
Pre: n is a nonnegative integer.
Post:
The function value is the factorial of n.
*/
int
factorial(int n)
{ if (n==0)
return 1;
else
return (n*factorial(n-1));
}
q Notice however, the memory required by this function
depends on the size of n. From one call
to the next, the system has to create an activation record in the system stack
(another application of stack) to hold the variables of the current call.
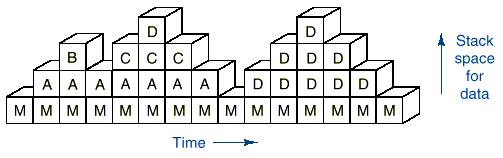
q Recursive calls (like other function calls) are
usually represented graphically using stack frames or recursive trees as shown by the following figures:
q Notice that the amount of memory required is
determined by the height of the recursive tree not by the number of recursive
calls.
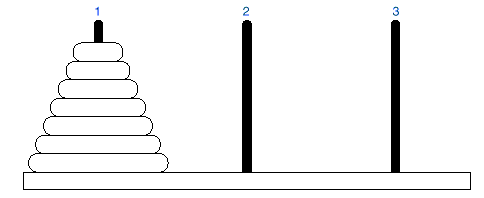
Example 2: Towers of Hanoi problem:
q Another popular example that demonstrates the use of
recursion is the Towers of Hanoi problem.
q It involves moving a number of disk stacked in order
of size from one pole (pole 1) to another pole (pole 3) using a middle pole
(pole 2) as a resting place. However,
the movement must be done such that a bigger pole is never put on top of a
smaller disk.
Solution.
q We observe that there is no way to reach the bottom
disk until all the other disks are on the middle pole. Similarly, moving the next largest from pole
2 to 3, we need to first move all the other disks to pole 1. This process, thus continue until we are
left with the smallest disk, which is paced directly on pole 3.
q The algorithm above can be implemented as follows:
/*
Move: moves count disks from start to finish using temp
for
temporary storage. */
void
Move(int count, int start, int finish, int temp)
{
if (count > 0) {
Move(count-1, start, temp, finish);
printf("Move a disk from %d to
%d.\n", start, finish);
Move(count-1, temp, finish, start);
}
}
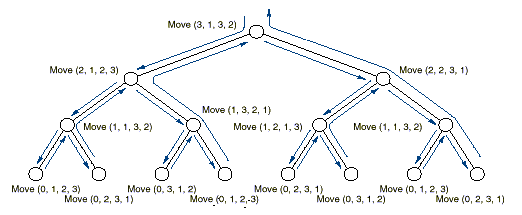
Analysis.
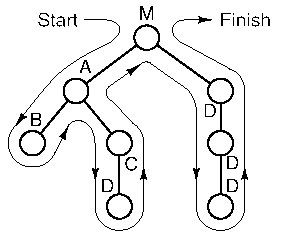
q The best way to analyze a recursive function is to
draw its recursive tree. This is shown
below for n=3.
q Notice that each recursive call reduces the number of
disks by 1. Thus, the
depth of the recursion is n.
q Notice also that except for the leaves, each recursive
call (vertex) results in two other recursive call.
q Thus, the number of non-recursive calls is given by
the series:
1+2+4+
… + 2n-1.