Sorting : Divide and Conquer methods
Objectives of this lecture
q Study (review) two divide
and conquer sorting methods; merge sort and quick sort
q Analyze the two methods and
compare their relative efficiency
Introduction:
q The basic characteristic of
quadratic sorting methods is that as the size of the list doubles, the running
time increases by a factor of four.
q The reverse however, is also
true. If list size is reduced by half,
the running time reduces by a factor of four.
q This fact suggests that
dividing a list into two and applying recursive divide and conquer approach
should reduce the sorting time.
q This is the idea behind
divide and conquer sorting methods which generally have the following form:
Sort(list)
{
if the list has length greater than 1 then
{
Partition the list into lowlist,
highlist;
Sort(lowlist);
Sort(highlist);
Combine(lowlist, highlist);
}
}
Merge Sort
q This consists of the
following steps:
Ø Split the list into two
equal (or nearly equal) sub-lists.
Ø Repeat the process on the
sub-list (recursively) until all the sub-lists are of order 1 – which means
they are already sorted.
Ø Rewind the recursion by
merging the sub-lists to form larger sorted list. At the end, the original list would have been sorted.
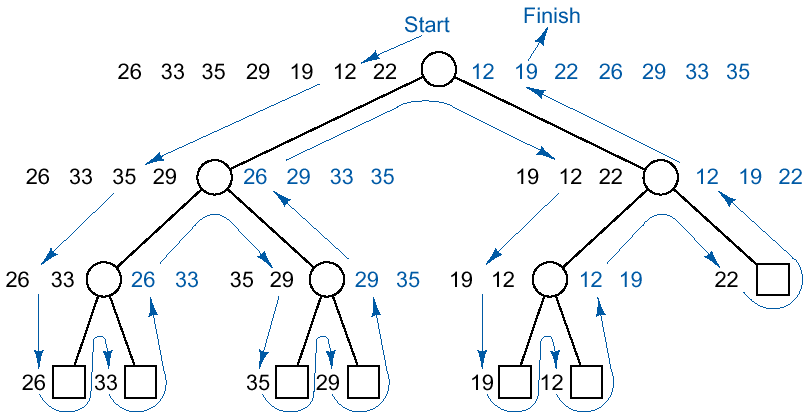
q The following recursive tree
traces merge sort using the list : 26 33 35
29 19 12 22
q The order in which recursion call occurs is indicated by the arrow:
q
Algorithm:
q The following program
implements merge sort
/* MergeSort: sort contiguous list by the merge sort
method.
Pre: The list has
been created. Each entry of list contains a key.
Post: The list have been sorted in into non-decreasing order.
Uses: Merge.
*/
void MergeSort(List *list, int first, int last)
{ int mid;
if(last >
first)
{ mid = (first
+ last)/2;
MergeSort(list, first, mid);
MergeSort(list, mid + 1, last);
Merge(list,
first, mid, mid + 1, last);
}
return;
}
/* Merge: merge two lists producing a third list.
Pre: first and
second are sorted lists and have been created.
Post: out is a sorted list containing all entries that
were in
first and
second.
*/
void Merge(List *list, int init1,int final1,int init2,int
final2)
{ int i,j,k;
ListEntry
temp[SIZE]; /* SIZE is a constant */
k = init1; i =
init1; j = init2;
while(i <=
final1 && j <= final2)
{ if (LT(list->entry[i].key,
list->entry[j].key)
temp[k++] = list->entry[i++];
else
temp[k++] = list->entry[j++];
}
while(i <=
final1)
temp[k++] =
list->entry[i++];
while(j <=
final2)
temp[k++] =
list->entry[j++];
for(k = init1; k
<= final2; k++)
list->entry[k] = temp[k];
return 0;
}
Analysis:
q First we notice that the
main work is being done by the merge function – this is where both the comparison and
data movement takes place.
q The number of comparisons in
the merge function depends on the
number of elements in the sub-list and their ordering. However, since all the elements must be
moved to temporary array and moved back to the sub-list, the number of moves is
twice the size of the sub-list.
q At the top-level for
example, at most n key comparison is made and 2n data movements.
q As we go down the recursive
levels, the size reduce by half each time, but the number of recursive calls
increase by the same factor so that the overall number of comparison is n at
each level as shown by the following diagram:
|
|
|
|
|
|
|
|
|
|
|
|
n
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x n/2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x n/4
|
q The total number of recursive
levels, k, is given by:
n = 2k è k = log n.
Thus,
number of comparisons = O(n log n) .
And
number of data movements = 2n log n = O(n log n).
q There is no best or worst
case, as the list has to be partitioned to simplest sub-lists always.
q One disadvantage of merge
sort is that a separate array of the same size as the original is required in
merging the sub-lists. This takes extra
space and computer time.
Quick Sort
q Quick sort is another
divide-and-conquer algorithm that spends more time in the partitioning step
than merge sort.
q It was developed by a
British Computer Scientist, C.A.R. Hoare
q To do the partitioning, Quick Sort first selects an element called
the pivot
and conceptually divide the list into two sub-lists with respect to the pivot:
the first sub-list consisting of all elements less than or equal to the pivot
and the second consists of all elements that are greater or equal to the pivot.
q These two sub-lists are then
sorted using the same idea. By the time
the list reduces to single elements, the list would have been sorted.
Partitioning
q There are many strategies
for partitioning the list, we shall adopt the following for its simplicity.
q We use two pointers, left and right which we initially set to
the first
and last
index and allow them to move towards each other.
q The left pointer is allowed
to increase until it reaches an element greater or equal to the pivot.
q Similarly, the right pointer
is allowed to decrease until it reaches an element less than or equal to the
pivot.
q Provided the pointers do not
cross, the elements they point to, are swapped and the pointers move
again. This process continues until the
pointers do cross at which stage the partition would have been achieved.
q We shall take the pivot to be the middle element.
q The following diagram
illustrates this idea.
Original list:
|
28 |
81 |
36 |
13 |
17 |
55 |
47 |
65 |
23 |
18 |
67 |
38 |
3 |
|
left |
|
|
|
|
|
|
|
|
|
|
|
right |
q First we choose a
pivot, the middle element = 47
q The left will move and stop
at 81 since 81>=47. The right however cannot move
since 3<=47. Thus, before swapping, we
have:
|
28 |
81 |
36 |
13 |
17 |
55 |
47 |
65 |
23 |
18 |
67 |
38 |
3 |
|
|
left |
|
|
|
|
|
|
|
|
|
|
right |
q We now swap the values to
obtain the following.
|
28 |
3 |
36 |
13 |
17 |
55 |
47 |
65 |
23 |
18 |
67 |
38 |
81 |
|
|
left |
|
|
|
|
|
|
|
|
|
|
right |
q Next left moves and stops at
55 since 55>=47. The right will moves at stops at 38
since 38<=47. Thus we have the following:
|
28 |
3 |
36 |
13 |
17 |
55 |
47 |
65 |
23 |
18 |
67 |
38 |
81 |
|
|
|
|
|
|
left |
|
|
|
|
|
right |
|
q We swaps these values to
obtain the following:
|
28 |
3 |
36 |
13 |
17 |
38 |
47 |
65 |
23 |
18 |
67 |
55 |
81 |
|
|
|
|
|
|
left |
|
|
|
|
|
right |
|
q Left moves and stops at 47 and right moves and stops at 18.
|
28 |
3 |
36 |
13 |
17 |
38 |
47 |
65 |
23 |
18 |
67 |
55 |
81 |
|
|
|
|
|
|
|
left |
|
|
right |
|
|
|
q We swap the values to
obtain:
|
28 |
3 |
36 |
13 |
17 |
38 |
18 |
65 |
23 |
47 |
67 |
55 |
81 |
|
|
|
|
|
|
|
left |
|
|
right |
|
|
|
q Left moves and stops at 65 and right moves and stops at 23. The two values are swapped to obtain:
|
28 |
3 |
36 |
13 |
17 |
38 |
18 |
23 |
65 |
47 |
67 |
55 |
81 |
|
|
|
|
|
|
|
|
left |
right |
|
|
|
|
q Finally, left moves to 65 and stops and right moves to 23 and stops.
|
28 |
3 |
36 |
13 |
17 |
38 |
18 |
23 |
65 |
47 |
67 |
55 |
81 |
|
|
|
|
|
|
|
|
right |
left |
|
|
|
|
q Since the pointers have
crossed, we stop. We now have a
partition in which all elements on the first sub-list are less than the pivot
and those on the second are larger than the pivot. These are:
|
28 |
3 |
36 |
13 |
17 |
38 |
18 |
23 |
|
65 |
47 |
67 |
55 |
81 |
|
|
|
q The algorithm is now applied
on these sub-lists and the process continues until the sub-lists reduces to one
element.
Algorithm
q The following program
implements this method.
void QuickSort(List *list, int start, int end)
{ int left = start, right = end;
ListEntry
pivot = list->entry[(start + end)/2];
partition(list, &left, &right, pivot);
if(start <
right)
QuickSort(list, start, right);
if(left <
end)
QuickSort(list, left, end);
}
void partition(List *list, int *left , int *right,
ListEntry pivot)
{ do
{ while(LT(list->entry[*left].key ,
pivot.key))
(*left)++;
while(GT(list->entry[*right].key,
pivot.key))
(*right)--;
if(*left < *right) /* if left did not cross right */
{
swap(&list->entry[*left] , &list->entry[*right]);
(*left)++;
(*right)--;
}
else if(*left == *right)
(*left)++;
}while(*left
<= *right);
}
void swap(ListEntry *a , ListEntry *b)
{
ListEntry temp;
temp = *a;
*a = *b;
*b = temp;
}
Analysis: