Indeterminacy of Long Run Equilibrium Values of Interest and Profit Rates
By
Dr. Usamah A Uthman
Associate Professor of Economics
Department of Finance & Economics
King Fahd University of Petroleum and Minerals (KFUPM)
Dhahran 31261
Saudi Arabia
E-mail : osama@kfupm.edu.sa
This paper won the best paper award ( the theoretical category ) at the conference on “Global Finance”, Istanbul, Turkey April 7-9, 1999. The author is grateful for Financial Support From KFUPM to complete this paper
Indeterminacy of Equilibrium Values of Interest and
Profit Rates
Abstract
This paper shows that Fisher’s defense of the classical position on the long term relationship between the interest rate and the profit rate is flawed. The existence of contractual interest in the economic system makes it indeterminate. Even if finance is to be done on profit sharing basis, the existence of the interest rate renders the system indeterminate. The two modes of finance can not coexist for the purpose of system determinacy, The removal of the interest rate make it determinate. (JEL B12, E43, G11, P43).
Introduction
The purpose of this paper goes beyond the history of economic thought. The stagnating economic problems in many parts of the world call for a reconsideration of some basic concepts of economics, in the hope that a better understanding of them shall make a better guidance for economic policy.
Classical economics theory considers the long-run interest rate a real variable determined by the profit rate on capital. The mechanism for achieving this is through the supply, and demand for savings. The classical theory also argues that interest is a measure of both the private and social marginal product of capital. It is thus considered the “price” of investible resources at which the demand for investment and the willingness to save are equated, leading to an optimal allocation of capital. Changes in the money supply are assumed to be neutral with respect to affecting the interest rate in the long run. In their demand for capital, businessmen compare the rate of profit that is expected to be made by the employment of it and the current market interest rate. Such a comparison is the decisive factor as to whether more or less of capital should be employed.
Perhaps, the clearest statement of the classical view on this issue is given by Ricardo. He writes:
“The interest of money is not regulated by the rate at which the Bank will lend, whether it be 5, 3, or 2 percent, but by the rate of profit which can be made by the employment of capital, and which is totally independent of the quantity or of the value of money. Whether the Bank lent one million, ten million, or a hundred million, they would not permanently alter the market rate of interest; they would alter only the value of the money which they thus issued. (Ricardo, 1951)
Keynes
argued that the classical contention of the equality between the marginal
efficiency of capital (or the profit rate) and the interest rate is true only
at equilibrium. “But to make this into a theory of the rate of interest
or to derive the rate of interest from it involves a circular argument, as
Marshall discovered as he got half-way into giving an account of the rate of
interest along these lines. For the marginal efficiency of capital partly
depends on the scale of current investment, and we must already know the rate
of interest before we can calculate what this scale will be” (Keynes, 1936, p.
184). In other words, the circularity argument can be represented by the
following flow chart:
|
Figure 1
|
|
|
|
|
|
This can be read as follows: The classicals claim that the marginal
efficiency of investment (MEI) affects the interest rate i, but we know
that interest affects investment, and investment affects MEI. It can thus
be said that interest, i, affects the marginal efficiency of capital,
MEI.
Irving Fisher (1930) defended the classical position saying that
“At first sight it may appear to those not familiar with the mathematics of simultaneous equations and variables that the reasoning is circular; the rate of interest depends on individual rates of impatience; these rates of impatience depend on the time shapes of individual income streams; and the choice of these time shapes of income streams depends, as we have just seen, on the rate of interest itself. It is perfectly true that, in this statement, the rate of interest depends in part on a chain of factors which finally depend in part on the rate of interest. Yet this chain is not the vicious circle it seems, for the last step in the circle is not the inverse of the first ... but the dependence, above stated, of interest on the range of options and the dependence of the choice among them on interest is not a case in point, for this last determining condition is not derivable form others."(1)
In other words, Fisher seems to say that the choice of investment opportunities and thus incomes there from, is not derivable from interest rates. And hence there is one circularity in the interest profit relationship. But we know for a fact of life that these interest rate adjusts much faster than real assets prices and hence faster than profits rates. This is going to be the case even in the most primitive economies. For when an investor or a consumer wants to decide on a potential endeavor he would compare the expected (profit) to the certain (contractual interest). Even though interest rates are continuously revised, they always represent the datum against which measurement of the desirability of investment of consumption is taken. In modern economies, it is the much greater divisibility and longevity of financial assets relative to real assets that contribute to the volatility of the interest rates for ahead of profit rates. It is for this volatility why governments try to influence the interest rate either through direct regulation or via the use of tools of monetary policy.
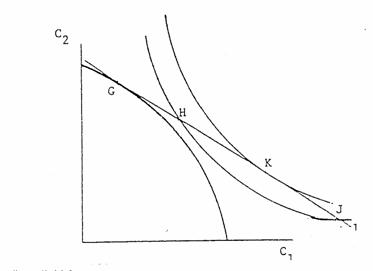
In the typical Fisherian model we are told that equilibrium is (figure 2) attained when the market interest rate, measured as the slope of the market line, the time rate of preferences, measured as the slope of the indifference curve at point K, and the profit rate, measured as the slope of the production possibility frontier at point G, are all equal (point K). Any deviation from that point causes the individual either to borrow (point H) or to lend (point J). (Dougherty, 1980, pp. 29-30). We are not told, however, how do we reach that equilibrium point. In particular, it is not clear what are the objects of trade that a lender and a borrower are exchanging.
Figure 2
Intertemporal equilibrium of production and consumption
|
|
|
|
|
|
|
Source:
Dougherty, 1980, the indifference curves are intertemporal with C1 and
C2 are consumption levels in t1 and t2 respectively.
It seems that Fisher’s line of reasoning imagines an individual who faces two choices, either to consume now, or save (and invest at the market interest rate) and consume later. But this discusses only one part of the story. The fact to the matter is that we have two individuals (the lender and the borrower) whose welfares are in direct conflict with each other, and where the income of one (the borrower) is only the residual of the other (the lender).
Criticisms of the Fisherian model have been based on attacking the various assumptions of that model. The determination of the plausibility of these assumptions (or the validity of these criticisms) is an empirical matter. My line of attack however is based on the logical structure of the model itself.
To do that, let’s assume that the Fisherian model can be looked at as a process of trading between a producer-borrower and a capitalist-lender. It is not clear what is it that they are trading. In the usual one-period, static model, two individuals exchange tangible endowments. Equilibrium is reached when the supply price and the demand price are equal. Both are expressed in tangible terms. When exchange over time (in the process of lending and borrowing) takes place, no such endowments exist in the first place. For although the lender offers a principal's sum to the borrower, it is not the object of exchange per se, as it is stipulated to be returned in full, later on, plus a mark-up. What a lender is actually offering is the abstinence from using that sum in the interim of the loan contract, in exchange for a promise by the borrower, to return the principal full and intact plus some mark-up. What we have here, thus, is an exchange of abstinence for a promise. But abstinence is hardly an object of exchange or a cause of reward as Fisher (1930) himself explained. While the interest rate represents a contractual measure of an ex post reward to the lender, it is not clear what the counter contractual measure of reward to the borrower is, if any.
To further show the dialectic relationship between the interest rate and the profit rate (assuming a stationary state of technology), a fall in interest rate causes profits (and the profit rate) on projects yet-to-be-taken to rise for two reinforcing reasons. First, there will be less discounting of profits at a lower interest rate (Samuelson 1966). Second, the fall in the interest rate implies lower interest payments on new debts, leaving a larger size of the residual profits and causing the profit rate to rise. Even though a decrease in the interest rate may be accompanied by a recession and a decrease in sales, the decrease in the interest rate helps to sustain profits. These two reasons shall always apply even if a change in interest rate may result in a reswitching2 of production techniques that may turn up a smaller gross output.3 The impact of the interest rate on the quantity of loanable funds demanded can be written as
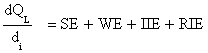
When SE is the substitution affect-a rise in the interest rate induces borrowers to substitute other modes of non-interest-based finance, or leisure for interest-based finance. A wealth affect, WE, is felt as a change in the interest rate affects the value of current assets but not the value of current liabilities, especially if those liabilities are not negotiable. In case of negotiable liabilities, the ability of the firm to call back its debt depends on its cash reserves among other things. There are two types of income affects to the interest rate. On type is the usual instantaneous income effect, IIE, if we assume that profits are known with certainty. But since interest payments extend over the future and they are fixed relative to variable uncertain profits, there is what can be called the relative income effect, RIE. The existence of the two income effects is unique to the interest rate. The impact of the interest rate investment may be far more than what first meets the eye.
Dougherty (1980) puts the circularity problem as follows. The value of capital goods is given by
V = ao + 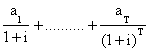
The neoclassical theory "pretends to offer an explanation of the determination of the rate of profit, and yet begins by assuming the knowledge o the rate of profit (or equivalently, its proxy, the real rate of interest.)” (P. 14). To put it differently, the problem is whether it is the rate of profit (determined by the marginal rate of capital) that is supposed to determine the value of individual capital goods, or is it the valuation of capital goods (at some interest rate) that determines the profit rate?
Dougherty dismisses the problem as a complete nonsense, contending that if two variables depend on each other that does not mean they are necessarily undetermined. The following example is given
Y = 2X
X = Y - 1
where two equations and two unknowns should resolve the problem of simultaneity and, give determinate values of X and Y. To Dougherty, and other neoclassical economists, the determination of equilibrium conditions and not the line of causality is the most important issue. Although, we do not submit to Dougherty’s argument for the reasons explained before, we can conclude from this that the circularity problem is actually a two-branch problem. First, there is the question of causality, and second, there is the question of determining the equilibrium values of the economic system. The more important of the two problems is not causality per se; for causality does not necessarily entail indeterminancy. Fisher and the neoclassicals are correct here. What is to be shown in this paper, however, is that the kind of circularity involved in the interest-profit relationship is an indeterminate one.
In what follows, a model is developed to show the indeterminate relationship between the interest and profit rates.
The Model 4
To start, one has to remember that while interest is a contractual form of income, profits are only a residual.
The demand for loanable funds for investment in the short run involves the comparison of the market interest rate and the expected gross profit rate. But since an investor realizes profits only after paying for his interest dues, it is the expected net profit rate that actually determines, along with the interest rate, his investment demand. This means that the demand for investment funds is a function of both variables. The former represents the cost (price) of getting the funds and the latter represents the actual (net) rate of return to the borrower. We can thus represent the demand function by the following equation:
ID = f(+N,-i).
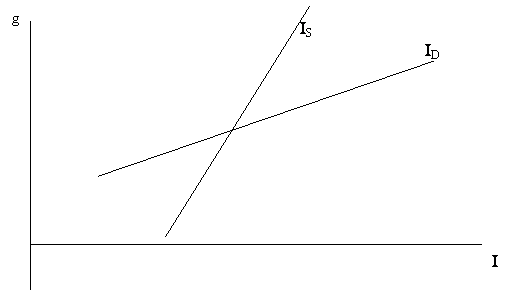
Where N is the expected net profit rate (or a proxy of MEI) and i is the interest rate5. Since in a, diagrammatic representation we usually link ID to i, the role of N in the above relationship is to locate the position of the schedule. N becomes a parameter, and analogous to y (income) in the Keynesian function I = f (i,y), or the Marshallian demand function Qd = f (p,y). We can thus say that N determines the position of the I = f (i) schedule. The lower the value of i, the greater the quantity of funds demanded for investment. This is a standard, traditional demand relationship applied to ID and i. Diagrammatically we have (Figure 3).
Figure 3.
Investment demand as a function of the interest rate and expected net profit rate.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
At any given
i, an increase in N (net profit) will lead to a higher demand for investment.
Problem : since we assume that N is equal to the gross profit rate,
g, minus the interest rate, where (N= g-i) how can an increase in N comes about
if there is no change in i6 ? Diagrammatically, we cannot know the
position of the ID schedule, unless we know N. But we
cannot know N unless we know i. But we cannot know i unless we know the
position of the schedule. So the interest –profit relationship is
indeterminate.
Mathematically speaking, the argument can be illustrated by the following simple model : 7
ID = f (N,i)
Is = h (i)
N = g- i
where N is the expected net (after-interest) profit rate, i is the interest rate, g is the, expected gross (pre-interest) profit. These are three equations but four unknowns: I, g, i, N. In the long run all of these variables are to be determined indigenously, so now of these can be assumed as given. No determinate equilibrium solution can be obtained.
If some finance is done on the basis of equity participation, while interest- based finance is still possible, interest payments disappear from these transactions, but the interest rate does not disappear from the model if transactors still watch for the interest rate as a signal on whether to invest in securities or in real investments. The model will collapse into the following two equations
ID = f (![]()
IS = h(![]()
The realized gross profits, g, will split between “borrowers” and “blenders”. We still have more unknowns than equations. Under the conditions explained above, both sides of finance will be effected positively by g, but negatively by i. A higher interest rate discourages borrowers from borrowing on the basis of contractual interest, while it discourages lenders from lending on the basis of profit shearing. If g is thought more important by both lenders and borrowers, then both schedules are positively slopped and i becomes a parameter as in figure 4. If both parties believe the other way around, then both schedules will be negatively stopped and g now is a parameter as in figure 5.
|
|
|
|
|
|
Figure 4 : g is
relatively more important and i is a parameter
|
|
|
|
|
|
Figure 5: i
is relatively more important and g is a parameter
One could imagine a situation under which either party, but not both, is concerned only with g, but not i. There would still be more unknown than equations. For example
ID = f (g)
IS = h (g,i)
If we introduce the profit share in the profit sharing scheme, while these profit shares may be compared to the market interest rate, we can write the model as follows:
ID = f(g,(1-µ), i)
IS = h(g, µ,i)
µ = k (g,i)
Where µ is the share of profits to be paid to the lender. The unknowns are I, g, i, and µ. The model is still indeterminate. If the interest rate disappears completely from the system, we shall have
ID = f(g,(1-µ))
IS = h(g, µ)
µ = k (g)
The system is determinate. It is obvious then that even if finance is done on the basis of profit sharing, the existence of the interest rate shall be a source of noise. The two modes of finance can not coexist if the economic system is to be determinate.
Chick (1984) explains that from a Keynesian macroeconomic point of view, the position of the speculative demand function (and hence the rate of interest) depends on the subjective reasons of opinion. The neoclassical position is that in the long-run equilibrium, the profit rate will adjust to some “normal” rate. If bulls and bears believe that this rate will persist long enough, the interest rate, then, will adjust itself in relation to that “normal” profit rate. As capital gains and losses disappear, real investment is enhanced and (or because) the speculative demand for money will also disappear (Chick, 1984).
Shackle (1968), however, falsifies this equilibrium scenario, arguing that, as it becomes believed that the interest rate will become constant, bears will try to buy bonds (and bulls hold on to theirs), thus driving up their prices and causing the rate of interest to fall. Shackle calls interest an inherently restless variable. One may argue that it is not obvious why and how should the profit rate adjust to some “normal” rate, and why should every one in the financial market, bulls and bears, come to the same kind of belief. Furthermore, the profit rate on real investments is determined over a much longer period of time than interest rates. It is not obvious why would all speculators hold on to the same kind of belief for a long period of time. If the profit rate and the interest rate could ever be in a long run equilibrium, why would some people tend to hold bonds while others tend to take the hustle of real investment?
In schempeter’s theory of the interest rate (1934), interest finds its explanation in the purchasing power of money. Since this power represents a “Voting power” in a capitalist economy, interest becomes the controlling price of all other prices. Or, in Schumpeter’s words, “it is the ephore” of the economic system. But when this is the case, the conditions of perfect competition are distorted. The monopolistic power of money as a resource reverses the line of causalitying in its favor. It boggles the mind to argue that the cost of an input does not affect profit. There is “a constant tendency in capitalism to reach beyond the limits of the availability of financing, in an attempt to avoid the limits of capital constraint”. (Dumenil & Levy, 1991) The demand for goods and services is not only affected by incomes of households, but also by finance from producers, sellers and bankers. A required rate of profit can only be sustained if credit to firms is matched by credit to consumers. Changes in the interest rate are bound to impinge on the profit rate from both the supply and the demand sides. If indeterminacy can occur, as our model suggests, without even the explicit accounting for monetary factors, it stands to reason that the latter is an accommodating (endogenous) factor that reinforces instability.
What I have tried to show in my model above, is that it is not only the subjective reasons of opinion that make the interest rate as inherently unstable, but there are also some objective reasons for such instability, besides those of the "mass psychology" and the "gambling casino". It is also obvious that it is not necessary to introduce monetary factors to establish the argument.
Summary
The classical theory considers the long-run interest rate a real variable determined by the rate of profit on capital. Changes in the money supply are thought to be neutral with respect to affecting the interest rate in the long run. Keynes vehemently rejected that argument, for the MEC depends on investment and we must already know the rate of interest before we can calculate what this scale will be. The classical defense rests on arguing that interdependency between variables does not necessary mean indeterminacy as can be shown by a set of simultaneous equations. There are thus two problems regarding the relationship between interest and profit. The first is the question of causality and the other is the question of determining the equilibrium values. The latter is the more important of the two.
An interest-based loan contract involves a peculiar kind of exchange. It implies the exchange of abstinence (by the lender) in return for a promise (by the borrower). But abstinence is hardly something to exchange as Fisher himself explained. A fall in the interest rate causes the profit rate to rise for two reinforcing reasons. First, there will be less discounting of profits.
Second, the fall in interest rate (and payments) leaves a larger size of the residual profits and raises the profit rate.
The model in this paper has shown diagrammatically that we cannot know the position of the investment schedule, ID, unless we know the rate of net profits, N. But we cannot know N unless we know the interest rate, i. But we cannot know i unless we know the position of the schedule (determined by the parameter N). So we are trapped in a circle.
The model has shown mathematically that equilibrium values cannot be obtained if there are more unknowns than there are equations. This, of course, shows that an indeterminate “solution” implies a dialectic relationship among the involved variables.
We may conclude that it is not only the subjective reasons of opinion that make the interest rate an inherently unstable variable, but there are also some objective reasons for such instability. The introduction of monetary factors is not necessary to establish the argument.
FOOTNOTES
1Keynes, whose “General Theory” appear in 1936 was definitely aware of Fisher’s (1930) defense of the classical positions on the relationship between interest and profit.
2Paul Samuelson (QJE, Nov. 1966) has shown that even when re-switching of techniques occurs (as a result of a fall in the interest rate) the real wage (which can be treated as a proxy for profits) - interest rate relationship will always be downward sloping. He explained that “under perfect competition either workers can hire capital goods or capitalists hire workers. At a lower interest rate, or cost of capital, workers can always pay themselves a higher real wage (by becoming capitalists themselves, I guess) even without changing techniques; so capitalists will have to match up”. In other words, an increase in the pre-discounted labor product, as interest rate falls and re-switching of techniques occurs, is not a necessary condition for a rising labor real wage as the interest rate falls. Samuelson, like many economists, used the term “interest” and “profit” interchangeably, thereby confusing the capitalist with the entrepreneur. Samuelson’s contention of perfect competition implies that under such conditions (of competition) the distinction between a worker and a capitalist is actually blurred if entry and exit between professions is free. But this does not tell us why somebody chooses one profession over another. The fact to the matter, of course, is that it is the individual's endowment (physical and mental) that decides for him his profession. This is besides the fact that as more workers hire capital goods, as Samuelson contends, the demand for capital goods increases, and the interest rate will be forced up, driving down the real wage for workers. The interest elasticity of real wage is an empirical matter.
3 An anonymous referee vehemently disagreed with me on this, contending that ‘this is simply double counting. For if an investment is worth undertaking at all, it is worth undertaking with borrowed money. If I use my own money, I demand the opportunity of value of tying it up in the investment as well as hoping to obtain a residual above that opportunity value. If I use someone else's money, all I get is the residual; but the total stream of benefits from the investment to someone axe precisely the same”. This is not quite accurate. For even if we grant the argument that the interest rate is a good measure of the cost of capital (whether owned or borrowed), debt and equity finance are not truly at par. If the market interest rate is 8%, say a person who owns the necessary funds for an investment and expects to get 8% (but no more), may go ahead and invest. But if he does not have these funds and he has to borrow at the going market rate and he expects that it will yield 8% (but no more), may in the world would he invest? Things will be worse if the actual rate of return turned to be less than the market rate. For in the case of equity, the actual loss is only the difference between the market and the realized rates. But in the case of debt, the loss is that amount plus the risk of foreclosure. The difference between equity and debt finance is that in the former case the investor owes the opportunity cost of capital to himself, while in the latter he owes it to someone else. They just cannot be at par!
4The model explained in this section is not meant to represent the Fisherian model of the relationship between profit and interest. It represents the author’s characterization of the problem.
5See Keynes (GT,1936, P. 137) for what determinates the inducement to investment.
6 By contrast, n the Marshalian demand function, a change in price is not a pre-condition for a change in the parameter y, income. Also n the short run i is comfort for current lane, but in the long run the interest rate has to change and he determined endogenously.
7 One should note that equilibrium is not assumed to have existed ex-ante. It is to be proven to exist, if possible.
REFERENCES
Chick, Victoria, Macroeconomics After Keynes: A Reconsideration of the General Theory, The MIT Press, Cambridge, Massachusetts, 1984.
Dougherty, Christopher, Interest And Profit, Methuen & Co. Ltd., London, 1980.
Dumenil, Gerard & Dominique Levey “The Classical legacy and beyond”, Structural Change and Economic dynamics, vol. 2, no.1, 1991
Fisher, Irving. The Theory of Interest (1930) Augustus M. Kelley Publishers, New York, 1970.
Keynes, John Maynard (1936) The General Theory of Employment, Interest, and Money, Harcourt, Brace & World, Inc., 1964.
Ricardo, David. The Works and Correspondence of David Ricardo (1817), Edited by Piero Srafa & Dobb, M.H. Cambridge, The University Press, 1951.
Shackle, G.L.S., “Recent Theories Concerning the Nature and Role of Interest”, Economic Journal 71, 1961. Reprinted in Surveys of Economic Theory, vol. 1, Macmillan, for the Royal Economic Society and the American Economic Association, 1968.
Samuelson, Paul “A Summing Up” Quarterly Journal of Economics 1966, 80(4).
Schumpeter, Joseph. A. The Theory of Economic Development, (with a new introduction by John E. Elliott), Transaction Publishers New Berunswich, U.S.A and London, UK (1934/1989)