|
Basic Concepts and Definitions
|
|
|
|
Background
Let us get the story of
"Frequency Domain" from the very beginning. You see, I and you being reasonable men,
believe that our world is three-dimensional in nature. But physicists, including
Albert Einstein and his likes, assert that the world is actually 4-dimensional,
the 4th dimension being TIME. Geophysicists, on the other hand, seem to have a
different opinion; they would like to work in a 5-dimensional world, the 5th
dimension, they insist, is FREQUENCY! They get this idea from a somewhat old but
admittedly very useful theory attributed to the French mathematician (Italy
claims he was Italian!) who goes by
the name: Jean Baptiste Joseph
Fourier. Here is an interesting clip of history to entertain
you and take boredom away:
 In 1798 Fourier joined
Napoleon's army in its invasion of Egypt as scientific adviser. While in
Cairo Fourier helped found the Cairo Institute and was one of the twelve
members of the mathematics division, the others included
Monge,
Malus and Napoleon Bonaparte. Fourier was elected secretary to the
Institute, a position he continued to hold during the entire French
occupation of Egypt. Fourier was also put in charge of collating the
scientific and literary discoveries made during the time in Egypt.
Fourier was not happy at the prospect of leaving the academic world and Paris but could not refuse Napoleon's request. He went to Grenoble where his duties as Prefect were many and varied. His two greatest achievements in this administrative position was overseeing the operation to drain the swamps of Bourgoin and to oversee the construction of a new highway from Grenoble to Turin. He also spent much time working on the Description of Egypt which was not completed until 1810 when Napoleon made changes, rewriting history in places, to it before publication. By the time a second edition appeared every reference to Napoleon would have been removed. It was during his time in Grenoble that Fourier did his important mathematical work on the theory of heat. His work on the topic began around 1804 and by 1807 he had completed his important memoir On the Propagation of Heat in Solid Bodies. The memoir was read to the Paris Institute on 21 December 1807 and a committee consisting of Lagrange, Laplace, Monge and Lacroix was set up to report on the work. Now this memoir is very highly regarded but at the time it caused controversy. There were two reasons for the committee to feel unhappy with the work. The first objection, made by Lagrange and Laplace in 1808, was to Fourier's expansions of functions as trigonometrical series, what we now call Fourier series. Further clarification by Fourier still failed to convince them, as was pointed out by a historian of the time:-
|
Well, that is the nature of the
history of science. Remember that there were vehement objections to the concept
of a spherical Earth orbiting the Sun when it was first introduce by
Galileo!
Basic Vocabulary of
Frequency Domain Analysis
Back to business; before we can discuss the matter of Frequency Domain at an intellectual level, let us build the essential vocabulary:
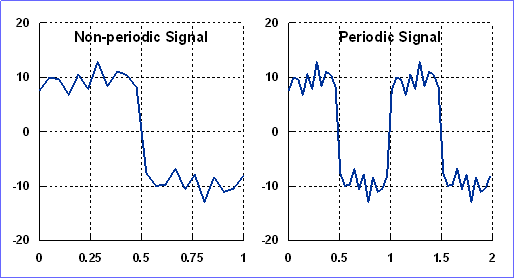 Signal: A geophysical signal is a function of space and/or time that represents a physical property of the Earth. Gravity, for instance, measured against distance from a reference point along a profile line is a signal. Non-Periodic Signal: (or Aperiodic), is one that is defined over a finite interval of space or time and vanishes outside that interval. Periodic Signal: One that repeats itself indefinitely with time or space. Mathematically, this is stated as: f(x) = f(x ± T) , T is called the period of the signal. We will have more about period later.
Period and Wave Length (T and/or l): If our signal is measured against time (ms, sec, hours, etc.) then we speak of PERIOD (Fig. a), which is the interval of time between tow identically located points on the signal. If, on the other hand, our signal is measured against distance (cm, m, km, etc.), then we speak of WAVE LENGTH in distance units. Cycle: Two identically located points on a periodic signal define one cycle of the signal. Note a cycle is neither a primary physical units nor does it have one. It is only a descriptive term (Fig b). Frequency (k): Is the number of repetitions (Cycles) of a periodic signal per unit time or distance. Comparing the two figures (a and b) to the right, you will notice that in the first the signal makes one cycle per unit measure, whereas in the second the signal executes two cycles in the same length of time/space unit. Hence, the former signal (a) has a frequency of 1 cycle/unit-measure and the latter (b) has a frequency of 2 cycles/unit-measure. Amplitude (A): It is illustrated in Figure (c) to the right. Amplitude is the height (depth) of the signal maximum (minimum) with respect to its zero-level. Amplitude is a measure of the energy in the signal. Phase (f): Examine Figure (d) and note how, compared to the blue signal, the peak of the orange signal is shifted with respect to the zero of the Time/Distance axis. We say that the two signals are out of phase. Phase is an angle and has the units of radians or degrees. Phase Shift: Is NOT the same as phase. It is phase angle per unit wave-number. The illustrations above are curves of the cos-functions which may be written as: S(q) = A cos [ k q ± f] The phase shift qs in this case is the value on the Time/Distance axis corresponding to the first peak of the signal. This is computed by setting the cos-function argument equal zero, which yields for the phase shift: qs = f / k |
Sinusoidal-Functions
At this point you may be wondering, since the argument of the cos-function is ordinarily an angle (measured in radians) , how could we speak of Time or Distance as an argument of a sinusoidal function? We manage to do this by the following argument:
Suppose we observe a signal over a time (distance) interval T (L). This (T or L) is, we assume, the basic (or fundamental) period of our observed signal. Now the SIN / COS functions have a basic period of 2p. Hence: q /2 p = x/L, or
q = (2 p / L) x
In terms of x, the sinusoidal function above may be written as:
S(q) = A cos [ w x ± f]
where: w = (2 p k/ L), is called the ANGULAR frequency.
The FUNDAMENTAL frequency of our observed signal is simply: fo = 1/L in Cycle/Distance (also called spatial frequency), and wo = 2pfo is the fundamental angular frequency in radians/Distance. k is called the wave number.
If the signal is a function of time, then we speak of TEMPORAL frequencies in cycle/unit-Time (also called Hertz or Hz).
Time, Space and Frequency
Domains
 Why do geophysicists want to work in the frequency world rather than the natural world? It turns out that many of the time-consuming and complex computations that we must do to process geophysical data are considerably simpler to perform in the frequency domain than in the time/space domains! Moreover, in the frequency domain, we can see more of the salient features of our signals that we can not otherwise see. Thus, in the frequency domain, we may easily reshape a signal, enhance parts (frequencies) of it and suppress unwanted others, isolate a primary signal from the influence of extraneous effects and much more. The next natural question is: How do we get into this Frequency Domain ? The answer brings us back to Jean Baptiste Joseph Fourier. Recall from the history clip that the objections "made by Lagrange and Laplace in 1808, was to Fourier's expansions of functions as trigonometrical series, what we now call Fourier series." It is this Fourier Series that, in modern applications, is used as a transform from Space/Time domains to Frequency domain and back. |
Fourier Series
Leaving aside mathematical formalities (conditions, etc.), here is what Fourier claimed and proved:
|
Any periodic signal may be broken up into an infinite number of smaller (simpler) signal each of which is characterized by its own amplitude, frequency and phase. This statement may be expressed mathematically in many ways, but the following are two of the more informative expressions:
Or, equivalently:
|
This sys that our original signal S(x) consists of an infinite sum of smaller and simpler signals the nth of which is:
with its unique amplitude, frequency and phase angle, An, wn and fn , respectively; and where:
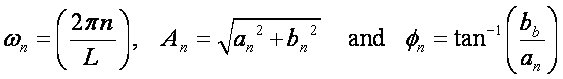
The a's and b's are computed from the following integrals:
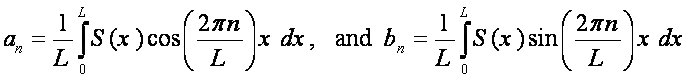
The details of how to apply these ideas to geophysical signals and how to compute the coefficients an and bn are discussed fully in class. What is important here, however, is to understand how we actually project our signal onto the Frequency Plane. This is a new vantage-point of looking at mathematical functions and it is important that you train yourself to think of signals from this view point.
Here is how you may envisage the transformation operation:
|
|
Once the signal is decomposed (analyzed) by the Fourier series into its constituent frequencies, we face the Frequency plane to see only a series of BARS and DOTS. The bars represent the amplitudes of the various Fourier terms and the dots (with values between ± p) are the associated phase angles. It should be obvious that in the frequency plane we do no see the wiggly curves that are so familiar to us in the Time/Space Plane - only dots and bars!
The Fourier Transform
Now you know that the Fourier Series is the tool to use for transforming PERIODIC signals from and to the Frequency Domain. But is it also suitable for the transformation of Aperiodic signals? The answer is an emphatic NO. The way we deal with non-periodic signals is to pretend that they are periodic with an infinite period and work our way from there. Starting with the integral definitions of the an's and bn's we take the limits as L => ∞ . If you do all the necessary mathematics [if you do not, see someone who has here Fourier Integral] you will end up with the following equivalent expression of the Fourier Series appropriate for transformation of APERIODIC signals:
Summary
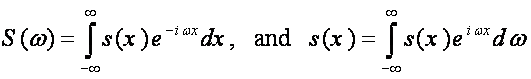
The table below summarizes the transforms that take us back and forth between the time/Space Domains and Frequency Domain. Details of their application and interpretation are covered in the course GEOP 205.
| Time & Space To Frequency Domains | Frequency To Time\Space Domain | |
| Periodic Signal |
|
Set up an LIP to recover S(x)
|
| Aperiodic Signal |
|
|
Further Reading
The following sites contain all the basic literature on the subject of Fourier Series and Integrals. Some sites have Java applets that give you an opportunity to experiment with these transforms. It is highly recommended that you visit some of the sites and examine the material given there.
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Discrete Signals |
