Subtraction involves having to represent negative numbers when the
subtrahend is larger than the minuend. One way of representing
negative numbers without the use of additional symbols is to represent
half of the combinations as negative numbers.
negative numbers
Suppose we use three decimal digits to represent numbers in our
system, then there are 1000 possible combinations of numbers from 000 to
999. We could allocate half of these, 000 to 499 for positive
numbers, and the remainder 500 through 999 as negative numbers.
What negative number does 999 represent?
When the odometer of a car reads 0999 and it goes through one more
kilometre, it then reads 1000. Note that the least significant 3
digits change from 999 to 000 and that is because 1 is added to
it. Therefore it is reasonable to expect that subtracting 1 from
000 will result in 999. Hence -1 is represented by 999, -2 by 998,
and so on.
Observing that 999 is 1000 - 1, 998 is 1000 - 2, and so on, we can
then obtain the negative representation by any negative number in our
system by subtracting it from 1000.
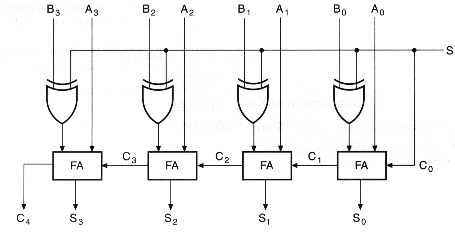
two's complements
In binary arithmetic two's complement arithmetic is the equivalent of
the above for the three digit decimal number system. Thus in the
4-bit two's complement number system, -1 is represented by 10000 - 0001
= 1111, -2 by 10000 - 0010 = 1110, and so on. However, not that
10000 is actually 1111 + 0001. Thus negative numbers can be
obtained by subtracting it from 1111 and then adding one.
However, note subtracting a number from 1111 will give its
complement. Hence two's complement is obtained by complementing
the number, and then incrementing by one. Two's complement of 4 in
the 4-bit number system is obtained by complementing 0100 as 1011, and
then adding 0001 to give 1100.
Now to subtract two numbers, we simply complement the minuend, and
then simply add it to the subtrahend to give the appropriate result.
adder-subtractor circuit