Copyright © 2004 Elsevier B.V. All rights reserved.
Effects of testing methods and conditions on the elastic properties of limestone rock
Department of Civil Engineering, King Fahd University of Petroleum and Minerals, Box 368, Dhahran 31261, Saudi Arabia
Received 13 August 2003;
Abstract
This paper presents results of a laboratory experimental program performed on limestone rock samples, using both static and dynamic methods. The objective is to compare elastic properties (elastic modulus and Poisson's ratio) for limestone rock, determined by static and dynamic methods, under different conditions. The static elastic modulus and Poisson's ratio were determined using cylindrical specimens tested under unconfined compression using a strain-controlled loading frame. Minor cycles of unloading–reloading were made at various stress levels. The data were analyzed to evaluate the effect of stress–strain level on the secant and tangent moduli as well as on Poisson's ratio. The values of the tangent modulus and Poisson's ratio during the minor cycles at various stress levels were also obtained. The dynamic elastic modulus and Poisson's ratio were determined for rock specimens using an ultrasonic system equipped with pairs of transmitting and receiving transducers: one P-wave and two polarized S-waves. Measurements were made at different confining pressures. The effects of cyclic loading, unloading, and reloading conditions were investigated. The static and dynamic results obtained for the investigated rock were analyzed and compared. The findings were also compared with similar results available in the literature for limestone rocks. The equivalent confinement to compensate for the cohesion was introduced to have a general form for the initial modulus that can be used even for cohesive materials at unconfined condition. For unconfined condition, the initial modulus is correlated with the unconfined compressive strength.
Author Keywords: Limestone rock; Static/dynamic modulus and Poisson's ratio; Cyclic loading; Confining pressure; Uniaxial compressive strength
Article Outline
- 1.
Introduction
- 2. Background
- 2.1. Literature review
- 2.2. Geology
- 2.3. Rock description
- 3. Experimental work
- 3.1. Static testing
- 3.1.1. Specimen preparation
- 3.1.2. Testing setup
- 3.1.3. Monotonic loading
- 3.1.4. Cyclic loading
- 3.2. Dynamic testing
- 3.2.1. Specimen preparation
- 3.2.2. Velocity measurement
- 4. Results and discussions
- 4.1. Static results
- 4.1.1. Results of monotonic loading
- 4.1.2. Results of cyclic loading
- 4.2. Dynamic results
- 4.2.1. Results of monotonic loading
- 4.2.2. Relationship between elastic modulus and confining pressure
- 4.2.3. Results of cyclic loading
- 4.3. Comparison between static and dynamic values
- 5. Conclusions
- Acknowledgements
- References
- 2. Background
1. Introduction
The elastic constants (elastic modulus and Poisson's ratio) are considered to be among the main fundamental mechanical properties of rock materials required for the analysis and design of engineering projects involving rocks. Limestone is a sedimentary rock encountered in many engineering projects worldwide. The elastic constants are extensively used in various formulations and modeling techniques, in order to predict the stress–strain behaviour of rocks subjected to various loading conditions. There are two ways of finding these constants: static and dynamic tests, each of which can be performed either in the field or in the laboratory.
In the laboratory, the static elastic constants are computed from the stress–strain response of a representative specimen of the material subjected to a uniaxial loading. The dynamic method is based on nondestructive geophysical (seismic/acoustic) testing. It involves the measurement of compression and shear wave velocities of a known frequency wave, traveling through a representative sample of the rock material. The elastic constants, based on the dynamic method (ultrasonic or logging), are widely used for hydraulic fracture design and wellbore/perforation stability evaluations in the petroleum industry.
It has been reported in the literature that the static and dynamic elastic moduli differ in values. There are many explanations proposed to explain this difference—ranging from strain amplitude effects to viscoelastic behavior. Additionally, this difference was explained as static measurements being more influenced by the presence of fracture, cracks, cavities, planes of weakness, or foliation (Zisman, 1933; Ide, 1936; Sutherland, 1962 and Coon, 1968). Investigation of such difference is still an active area of research, to understand the various contributing parameters and to enable a better interpretation of the mechanical properties from wave velocity measurements. The existence of some discrepancy in the values of these constants between static and dynamic methods as reported in the literature requires good judgment and further investigation of the methods used to determine these constants. Also, the relationships between the constants determined from the two methods need to be evaluated.
This paper presents results of a laboratory experimental program performed on limestone rock samples, using both static and dynamic methods. The objective is to compare elastic properties (elastic modulus and Poisson's ratio) for specimens obtained from a limestone rock outcrop in Saudi Arabia, as determined in the laboratory using the static and dynamic methods. For static method, the effects of cyclic loading and stress–strain level on the values of the elastic properties were investigated. For dynamic method, the effects of confining pressure and cyclic loading were also studied.
2. Background
2.1. Literature review
There is no consensus in the literature on an exact definition of the static Young's modulus, or on a method that can uniquely determine it. The static modulus is usually determined according to ASTM D 3148 standard, which states that the axial modulus may be calculated using any one of several methods employed in engineering practice, such as:
- 1) the tangent modulus at a stress level, which is some fixed percentage
of the maximum strength;
- 2) the average slope of the straight line portion of the stress–strain curve;
- 3) the secant modulus, from zero stress to some percentage of maximum strength.
- 2) the average slope of the straight line portion of the stress–strain curve;
The static method gives rise to a large scatter of results, but it can provide results at high strains (10−2) that occur in the mining industry. On the other hand, the dynamic method involves a smaller scatter of results, but these belong to the low strain category (10−5). Because of that, Vutukuri et al. (1974) concluded that a comparison of static and dynamic moduli is meaningful only if the values of the static modulus are taken at low strain–stress levels (i.e., using the initial tangent modulus).
The relationships between static and dynamic elastic properties have been studied since the early 1930s when techniques involving the propagation of acoustic waves were used in the characterization of rocks in mining, petroleum, and geotechnical engineering. Dynamic measurements are often used because they are easy to obtain and are nondestructive. Also, there are rarely enough cores available for the static method.
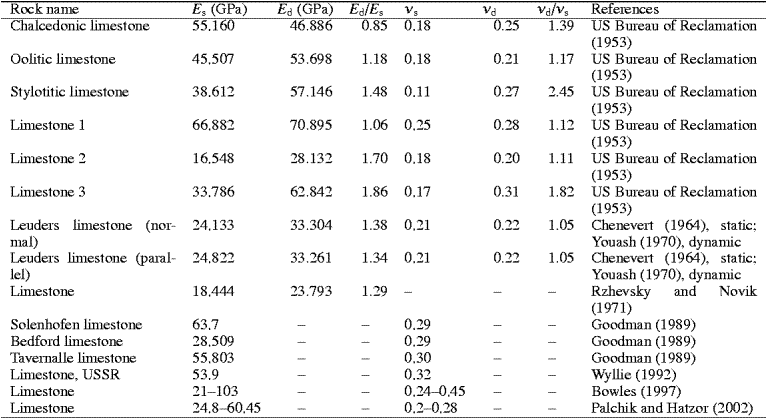
The ratio of the dynamic modulus (Ed) to static modulus (Es) reported in the literature for limestone rocks varies between 0.85 and 1.86 (Table 1). This ratio is usually large for rocks having a small modulus of elasticity (GRI, 1992). However, for rocks with a high modulus of elasticity, this ratio is low and may be less than 1.0. Various forms of correlations between Ed and Es reported in the literature are given below (both expressed in gigapascals).
King
(1983) reported the results of 174 measurements of the static elastic
modulus (Es) as a function of the dynamic elastic modulus
(Ed) for igneous and metamorphic rocks from the Canadian
shield. Using linear regression, the following relationship was
reported:
Van
Heerden (1987) tested 10 different types of rocks, and he found that in most
cases, Ed is greater than Es, but the
dynamic Poisson's ratio (νd) is smaller than the static
Poisson's ratio (νs). Results were fitted by the following
relationship:
Eissa
and Kazi (1988) obtained the following relationships:
They concluded that the correspondence between the two moduli (Eq. (3) is rather low. A better estimate was found by including the rock density (ρ;, g/cm3) in the relationship (Eq. (4).
Goodman (1989) indicated that the tangent modulus obtained from the loading curve contains both recoverable and nonrecoverable strains. In general, whenever the modulus value is calculated directly from the slope of the rising portion of a virgin loading curve, the determined property should be reported as a modulus of deformation rather than a modulus of elasticity. Unfortunately, this is not universal practice at present. He concluded that the elastic constants (elastic modulus and Poisson's ratio) should be defined with respect to the reloading curve.
Plona and Cook (1995) investigated the effect of stress cycles on static and dynamic moduli for sandstone. They have shown that the static Young's modulus, when consistently defined in terms of small amplitude, is similar to the dynamic Young's modulus measured along the stress direction. They also demonstrated that major and minor stress–strain cycles are useful tools to explore the relationships between static and dynamic properties of rocks.
2.2. Geology
The investigated limestone rock belongs to the “Khuff” formation, which relates to the early Triassic to late Permian age [215–270 million years before present (MYBP)]. The structural geology for this formation indicates that it outcrops at various places in the Central Province of Saudi Arabia, with an altitude reaching some hundreds of meters above sea level, and it dips toward the east to a depth of about 2000–4000 m below sea level in the Eastern Province (Powers et al., 1963). Fig. 1 gives a general structural geology of sedimentary rock formations in Saudi Arabia, including the Khuff formation. Fig. 2 shows photos of a side of a new highway cut made through the outcrop of this formation at the Gassim area of Saudi Arabia. These photos indicated the layering nature of this limestone formation, and the variation of the thickness of layers. This makes it difficult to obtain a representative sample for the entire formation. Rock blocks were collected from the thick layers found in the face of the cut. The orientations of the blocks were marked in the site, and they were transported to the laboratory for specimen preparation.
.gif)
| Full-size image (43K) |
Fig. 2. Highway cut through the outcrop of Khuff formation, rock sample collection site.
2.3. Rock description
Preliminary studies showed that this rock is a very homogeneous, beige-colored, muddy limestone. It is extremely dense and lacks any visible pores under a polarizing microscope. The physical properties include a dry density of 2586 kg/m3, a specific gravity of 2.737, a void ratio of 0.055, and a porosity of 5.4% (Al-Shayea et al., 2000). The tensile strength (σt) of this limestone rock was found to be 2.31 MPa (Khan and Al-Shayea, 2000). The mineralogical composition of this rock determined by X-ray diffraction (XRD) analysis (Fig. 3) indicates that this rock is very pure limestone (99% CaCO3).
3. Experimental work
3.1. Static testing
3.1.1. Specimen preparation
Cylindrical specimens of 23.5 mm in diameter were drilled from the rock blocks described above. The drilled specimens were cut into lengths of 50.8 mm, using a high-speed rotary saw. The ratio of length to diameter is maintained at greater than 2. The end faces of the specimens were ground using an end-face grinder, and then checked for evenness and perpendicularity with respect to the vertical axis. At the midheight of each specimen, two small strain gauges were attached: one along the length (vertical) and one along the circumference (horizontal). The strain gauges were the GFLA-6-50 type (Tokyo Sokki Kenkyujo, Japan).
3.1.2. Testing setup
A strain-controlled loading frame, having a capacity of 100 kN, was used for the load application (Fig. 4). The frame is equipped with a load cell to measure the applied load, and with an LVDT (Linear Variable Differential Transformer) to measure the vertical displacement. Rock specimen was mounted under the loading frame. The load cell, the LVDT, and the strain gauges were connected to a computerized data logger (TDS-303 type; Tokyo Sokki Kenkyujo). All measuring devices were calibrated, and the tests were made according to ASTM Standard D 3148-86 (ASTM, 1993).
3.1.3. Monotonic loading
For specimens 1 and 2, the load was gradually applied at a rate of 0.0021 mm/s, until the specimen failed. The applied load, the vertical displacement, and the vertical and horizontal strains were continuously recorded during loading.
3.1.4. Cyclic loading
Another specimen was tested under cyclic loading. The load was gradually applied at a rate of 0.0021 mm/s to a certain level, and slight unloading–reloading cycles were applied. This test included three cycles of about 5–10% of qu, at different stress levels, before the specimen failed. The applied load, the vertical displacement, and the vertical and horizontal strains were continuously recorded during loading.
3.2. Dynamic testing
3.2.1. Specimen preparation
Cylindrical specimens of 38 mm (1.5 in.) in diameter were drilled from the rock blocks described above. Then the drilled specimens were cut into 23±2 mm (1.0 in.) lengths, using a high-speed rotary saw. These dimensions are in accordance with the specification of the testing method. The end faces of the specimens were ground using an end-face grinder. The end faces were checked for evenness and perpendicularity with respect to the vertical axis of the specimen, using a V-block and a dial gauge.
3.2.2. Velocity measurement
For velocity measurement, an Autoplab 500 ultrasonic system (NER) was used. The schematic of the system is shown in Fig. 5, which consists of an ultrasonic transducer assembly and a metallic safety enclosure. A pressure vessel mounted inside the safety enclosure is connected to two hand pumps mounted on the sides of the safety enclosure. One of the pumps with an intensifier serves the purpose of pressurizing the confining fluid. The transducer assembly has one P-wave pair and two polarized S-wave pairs of transmitting and receiving transducers. The transducers, with a central frequency of 700 kHz, are housed inside stainless steel platens.
Before testing, the density of the specimen was measured. Then, the specimen was mounted in the system as follows. A shear wave couplant was applied at the end faces of the rock specimen, and then the specimen was slipped into a rubber sleeve. The rubber sleeve, along with the specimen, was placed between the platens of the transducer assembly in a way to ensure a good contact between the platens and the specimen's faces. Steel clamps tightly clamped both ends of the rubber sleeve against the platens. Then transducer assembly was slipped inside the pressure vessel. Light oil was poured into the pressure vessel as a confining fluid, and the sample was pressurized to the desired level.
At one end of the rock specimen, the transmitting traducers excited P- waves and S-waves, and then these signals were received at the other end of the specimen by the receiving transducers. A Unix-based software controls the excitation and transmission of the wave, and the data are stored in a personal computer. Velocity measurements were made at different confining pressures, as the confining pressure was increased (loading) and also as the confining pressure was decreased (unloading). Tests were made in accordance with ASTM Standard D 2845-90 (ASTM, 1993).
4. Results and discussions
4.1. Static results
4.1.1. Results of monotonic loading
Fig.
6 shows the stress–strain relationships of two rock specimens, tested under
a monotonic unconfined compressive load. The variation of vertical stress is
presented with both vertical and horizontal strains (![]() v and
v and ![]() h). The unconfined compressive strength measurements of
specimens 1 and 2 were 102 and 107 MPa, respectively.
h). The unconfined compressive strength measurements of
specimens 1 and 2 were 102 and 107 MPa, respectively.
The static tangent modulus (Etan) was obtained as the first
derivative of the vertical stress (σ) with respect to the vertical strain
(![]() v). First, a formula was produced to describe the
relationship between the vertical stress (σ) and the vertical strain
(
v). First, a formula was produced to describe the
relationship between the vertical stress (σ) and the vertical strain
(![]() v), for each of the stress–strain curves shown in Fig.
6. Then this formula was differentiated with respect to
v), for each of the stress–strain curves shown in Fig.
6. Then this formula was differentiated with respect to ![]() v to obtain the static tangent modulus
(Etan):
v to obtain the static tangent modulus
(Etan):
Fig. 7 shows the variation of the static tangent modulus (Etan) with the vertical stress level. The vertical stress level is defined as the vertical stress (σ) normalized to the respective unconfined compressive strength (qu) of the specimen. Etan increases with increasing qu percent until a certain level, beyond which it starts to decrease. For specimen 1, Etan increases from an initial value of 54.8 GPa until a value of 61.0 GPa at qu%=39%, then it starts to decrease until a value of 45.9 GPa just before failure defined by the crushing of the specimen. For this specimen, failure occurred at a sudden brittle fashion, without a significant plastic deformation, not allowing Etan to approach zero. For specimen 2, Etan increases from an initial value of 33.727 GPa until a value of 50.1 GPa at qu%=37.5%, then it starts to decrease, approaching zero to a value of 9.6 GPa just before failure.
Fig.
8 shows the variation of the static Poisson's ratio (νs)
with the vertical stress level. The Poisson's ratio is the negative of the ratio
of the horizontal strain to the vertical strain, as measured by the strain
gauges:
Table 2 gives a summary of the values of the static elastic constants (Etan, Esec, and νs) at various percentages of the stress level (% qu), in which Esec is the secant modulus. The elastic modulus obtained from the slope of the straight line portion of the stress–strain curve was found to be about 60 and 49 GPa for specimens 1 and 2, respectively. These values are close to those of the tangent modulus at a stress level equal to 50% qu. The values of the elastic constants obtained from this study are within the ranges reported in the literature for limestone rocks (Table 1).
The modulus ratio (E/qu) is the ratio of elastic modulus to the unconfined compressive strength, which is used in classifying intact rock specimens. This ratio was about 590 and 450 for specimens 1 and 2, respectively. For most rocks, the E/qu ratio lies between 200 and 500, but extreme values range as widely as 100–1200. In general, the modulus ratio is higher for crystalline rocks than for clastic rocks (Goodman, 1989).
4.1.2. Results of cyclic loading
Fig. 9 shows the stress–strain relationships for the rock specimen tested under unconfined compressive load with three small cycles of unloading and reloading at different stress levels. The unconfined compressive strength was 76.2 MPa. Table 3 gives the values of the tangent modulus (Etan) and Poisson's ratio (νs) at different stress levels (for loading, unloading, and reloading conditions). Fig. 10 and Fig. 11 give the variation of the static tangent modulus (Etan) and the Poisson's ratio (νs), respectively, with the vertical stress level.
Table 3. Values of static tangent modulus and Poisson's ratio at loading, unloading, and reloading conditions
.gif)
.gif)
| Full-size image (7K) |
Fig. 10. Static tangent modulus vs. vertical stress from cyclic unconfined compressive test.
.gif)
| Full-size image (6K) |
Fig. 11. Static Poisson's ratio vs. vertical stress from cyclic unconfined compressive test.
Fig. 10 shows that the tangent modulus at the unloading and reloading conditions is higher than that at the loading condition. This difference increases with increasing stress level, from about 35% at the first cycle (at a stress level of about 33% qu) to about 137% at the third cycle (at a stress level of about 88% qu). The tangent modulus obtained from the unloading–reloading curves is higher in value and has less variation than that obtained from the loading curve. Furthermore, the tangent modulus obtained from the unloading curve is higher in value and has less variation than that obtained from the reloading curve; it is almost constant regardless of the stress level.
On the other hand, Fig. 11 shows that the Poisson's ratio is less affected by the conditions of loading, unlading, and reloading. This is ascribed to the fact that the nonrecoverable strains exist in both the horizontal and vertical components of the strains that are used to compute the Poisson's ratio. The Poisson's ratios obtained from the loading and unloading curves have less variation than that obtained from the reloading curve.
4.2. Dynamic results
From the velocity measurements of the P-waves and S-waves
(VP and VS, respectively), the dynamic
elastic modulus (Ed) and the dynamic Poisson's ratio
(νd) were determined according to:
.gif)
.gif)
4.2.1. Results of monotonic loading
The variations of the dynamic elastic modulus and the dynamic Poisson's ratio
with respect to the confining pressure (σc) are shown in Fig.
12 and Fig.
13, respectively. These variations are best fitted by the following
quadratic polynomials:
where Ed is in gigapascals and σc is in megapascals.
The values of Ed and νd for an unconfined condition (σc=0) were found by extrapolation to be 44.1 GPa and 0.233, respectively. The value of Ed is found to increase monotonically with σc to a value of 52.0 GPa at σc=70.5 MPa. This increase amounts to about 17.9%. Notice that this value of σc is close to the value of qu for this rock material. On the other hand, the value of νd (Fig. 13) is found to increase monotonically with σc to a value of 0.262 at σc=70.5 MPa. This increase amounts to about 12.4%. Another rock specimen tested at a low confining pressure of 1.1 MPa produced a value of Ed equal to 48.08 GPa and a νd value of 0.281.
4.2.2. Relationship between elastic modulus and confining pressure
Because Ed is obtained at very low stress–strain level, it
represents the initial tangent modulus. According to Janbu
(1963), the initial tangent modulus (Ei) for soils is
assumed to increase with the confining pressure (σc) according
to the following exponential form:
.gif)
| Full-size image (10K) |
Fig. 14. K and n parameters for the variation of initial tangent modulus with confining pressure.
However, Eq.
(11) represents the case of cohesionless soils, and it deteriorates for the
case of no confinement (σc=0). For the case of cohesive
materials (rocks, cohesive soils, or concrete), Eq.
(11) needs to be modified so that Ei has a nonzero value
at the unconfined condition. This can be achieved by introducing an equivalent
confinement (σe) that needs to be added to the applied
confining pressure (σc) to compensate for the cohesion. The
modified form for Ei is recommended to have the following
form:
The equivalent confinement (σe) can be determined using
Mohr circle and Mohr–Coulomb failure envelope, as represented in Fig.
15. From those for the case of unconfined compression (the solid circle and
envelope; Fig.
15), it can be shown that the cohesion (C) for cohesive materials
(rock, cohesive soil, or concrete) can be expressed in terms of the unconfined
compressive strength (qu) as follows:
.gif)
| Full-size image (9K) |
Fig. 15. ![]() and
and ![]() parameters for the variation of initial
tangent modulus vs. confining pressure, with cohesion considered.
parameters for the variation of initial
tangent modulus vs. confining pressure, with cohesion considered.
From the static tests (Section 4.1.1), the angle of inclination of the failure plan (θ) was found to be about 67.5° and 64.5° for specimens 1 and 2, respectively (see broken specimen; Fig. 4). Using Eq. (14), the angle of internal friction (φ) has an average value of 42°. This is within the typical range of values for φ reported in the literature for limestone rock, which is 34.8–45Goodman, 1989 and Bowles, 1997. Using the average value of qu for specimens 1 and 2 (105 MPa) and their average value of φ (42°) in Eq. (13), the average cohesion (C) is 0.223qu=23.3 MPa.
From Eq.
(13), the value of the cohesion normalized to the unconfined compressive
strength (C/qu ratio) is a function of the angle of
internal friction (φ) only, and has the following form:
.gif)
The variation of C/qu ratio vs. the angle of internal friction (φ) is depicted in Fig. 16 (solid line). For a range of values of φ between 30° and 60° for rocks, the corresponding range of value of C/qu ratio is 0.289 and 0.134, respectively.
.gif)
| Full-size image (7K) |
Fig. 16. Variation of C/qu and σe/qu ratios vs. the angle of internal friction (φ).
From Fig.
15, the equivalent confinement (σe) can be shown
as:
Substituting Eq.
(16) into Eq.
(13) yields:
Using the average value of qu for specimens 1 and 2 (105 MPa) and their average value of φ (42°) in Eq. (17), the equivalent confinement (σe) is 0.247qu=25.9 MPa. Notice that the value of σe=Ccotφ is much greater than the tensile strength (σt=2.31 MPa) of this limestone rock, which is in accordance with the tension cutoff superimposed on the Mohr–Coulomb failure criterion in the negative region (Goodman, 1989).
From Eq.
(17), the value of the equivalent confinement normalized to the unconfined
compressive strength (σe/qu ratio) is a
function of the angle of internal friction (φ) only, and has the
following form:
.gif)
The variation of σe/qu ratio vs. the angle of internal friction (φ) is also depicted in Fig. 16 (dashed line). For a range of value of φ for rocks between 30° and 60°, the corresponding range of value of σe/qu ratio is 0.5 and 0.077, respectively.
For the case of no confinement (σc=0), the initial tangent
modulus (Ei) for the tested rock can be calculated from Eq.
(12) in terms of unconfined compressive strength:
This gives a value of Ei equal to 44.2 GPa, which compares well with the value of Ed found by extrapolation (Fig. 12 or Eq. (9)) to be 44.1 GPa.
Eq. (19) has a similar form to that used to calculate the modulus of elasticity for normal-weight concrete (Ec), as given by Ec=4700(fc′)0.5, where fc′ is the unconfined compressive strength for concrete and both Ec and fc′ are in megapascals (ACI, 1989).
Eq. (12) with the equivalent confinement (σe) given by Eq. (17) is general in nature and can be used for any material, including the cohesive materials (rock, cohesive soil, or concrete). The effect of considering the cohesion is equivalent to shifting the Mohr circle and the Mohr–Coulomb failure envelope (Fig. 15) along the horizontal axis by a magnitude equal to σe (the dotted circle and envelope), and maintaining the same value of φ. As a special case of cohesionless materials, qu=0 and, consequently, σe=0, which makes Eq. (12) boil down to Eq. (11).
Adding the value of σe=25.9 MPa to the confining pressure,
the values of Ed from Fig.
12 were replotted also in Fig.
14 (solid circles and line). The modified parameters, ![]() and
and ![]() (in Eq.
(12)) for the tested rock sample are 216,357 and 0.127, respectively. Notice
that
(in Eq.
(12)) for the tested rock sample are 216,357 and 0.127, respectively. Notice
that ![]() it is less than K, but
it is less than K, but ![]() is greater than n.
is greater than n.
4.2.3. Results of cyclic loading
The effects of increasing and decreasing the confining pressure (loading and
unloading) on Ed and νd were studied by
testing another rock specimen under such cyclic loading. The results for
Ed and νd are shown in Fig.
17 and Fig.
18, respectively. The best fitting is a quadratic polynomial of the
form:
.gif)
These constants are shown in Table 4, and they are comparable with those of (9) and (10). The values of Ed obtained from Fig. 17 by extrapolation at σc=0 are 41.3 and 42.6 GPa for loading and unloading conditions, respectively. Notice that the values during unloading are slightly higher than those during loading by a maximum of 3.3%. The value of Ed increases monotonically with σc to a value of 51 GPa at σc=80 MPa. This increase amounts to about 23.5%. On the other hand, the value of νd obtained from Fig. 18 by extrapolation at σc=0 is 0.223 for both loading and unloading conditions. The values during unloading are slightly higher than those during loading. The value of νd increases monotonically with σc to a value of 0.258 at σc=80 MPa. This increase amounts to about 15.7%.
The values of Ed from Fig.
17 were replotted in Fig.
19 using a log–log scale, with the value of σe=25.9 MPa
being added to the confining pressure. The modified parameters ![]() and
and ![]() in Eq.
(12) for the tested rock sample are 176,176 and 0.152, respectively, for
loading condition, and 210,046 and 0.127, respectively, for unloading
condition.
in Eq.
(12) for the tested rock sample are 176,176 and 0.152, respectively, for
loading condition, and 210,046 and 0.127, respectively, for unloading
condition.
.gif)
| Full-size image (9K) |
Fig. 19. ![]() and
and ![]() parameters for the variation of initial
tangent modulus vs. confining pressure with cohesion considered, from cyclic
test.
parameters for the variation of initial
tangent modulus vs. confining pressure with cohesion considered, from cyclic
test.
4.3. Comparison between static and dynamic values
The dynamic values of Ed and νd obtained from Fig. 12 and Fig. 13 by extrapolation at σc=0 (44.1 GPa and 0.233, respectively) compare well with the average static values of Es and νs at the initial state of loading, which are 44.2 GPa and 0.224 (for specimens 1 and 2; Table 2).
The values of Es determined by the three different methods proposed by ASTM vary by as much as 20%. Therefore, comparison between the results of the static and dynamic methods will be more meaningful after establishing a reliable and replicable method for determining the static modulus of elasticity. The ratios of Ed/Es and νd/νs are within the ranges reported in the literature. Because of the high strength and low porosity of the investigated rock, the value of Ed/Es is about unity.
The static properties are more scattered than the dynamic ones. The scatter in the values of the static and dynamic elastic properties is ascribed to lithological variation and the distribution of microcracks in the rock materials. Additional causes of further scatter in the case of the static properties can be attributed to any misalignment during sample preparation and mounting, which leads to loading eccentricity.
Cyclic loading affects the static tangent modulus much more than the dynamic modulus. The difference in the value of the static tangent modulus between the unloading and reloading conditions is about 137% at a stress level of about 88% qu. The values of Ed during unloading are slightly higher than those during loading by a maximum of 3.3%.
5. Conclusions
The values of the static elastic constants (Es and νs) are not constants, but are functions of the stress–strain level. The value of Es increases with an increase of the stress–strain level to a maximum value, beyond which it starts to decline. The increase in Es is attributed to the increase in the density and closure of microcracks following compression. The decrease in Es after that is attributed to the induced damage that degrades the integrity of the rock material. The changes in these mechanical properties are reflections of the continuous changes in the physical properties of the rock material during loading, especially those attributed to permanent deformation.
The values of Es determined by the three different methods proposed by ASTM vary by as much as 20%. Therefore, there is still a need for the establishment of a reliable and replicable method for determining the static modulus of elasticity. The comparison between the results of the static and dynamic methods will have more meaning after the establishment of such a method. The ratios of Ed/Es and νd/νs are within the ranges reported in the literature. Because of the high strength of the investigated rock, the value of Ed/Es is about unity.
The scatter in the values of the static and dynamic elastic properties is ascribed to lithological variation and the distribution of microcracks in the rock materials. Additional causes of further scatter in the values of the static properties can be attributed to the sensitivity of these properties to any misalignment during sample preparation and mounting, which may have produced some loading eccentricities.
The elastic constants (elastic modulus and Poisson's ratio) should be defined with respect to the unloading–reloading curves at a specific value of the stress level (% qu), not with respect to the loading curve that contains both recoverable and nonrecoverable strains.
Cyclic loading indicates that the static tangent modulus during the unloading and reloading conditions is higher than that at the loading condition. This difference increases with increasing stress level, from about 35% at a stress level of about 33% qu to about 137% at a stress level of about 88% qu. The tangent modulus obtained from the unloading–reloading curves is higher in value and has less variation than that obtained from the loading curve. Furthermore, the tangent modulus obtained from the unloading curve is higher in value and has less variation than that obtained from the reloading curve; it is almost constant regardless of the stress level. On the other hand, the static Poisson's ratio is less affected by the conditions of loading, unloading, and reloading.
The value of Ed is found to increase with σc from 44.1 GPa for unconfined condition to 52 GPa at σc= 70.5 MPa—a 17.9% increase. On the other hand, the value of νd is found to increase with σc from 0.233 for unconfined condition to 0.262 at σc=70.5 MPa—a 12.4% increase. Under cyclic loading, the values of Ed and νd during unloading are slightly higher than those during loading.
The introduction of the concept of the equivalent confinement (σe) to compensate for cohesion made a contribution to a general form for the initial modulus (Eq. (12) that can be used for any material, including the cohesive (rock, cohesive soil, or concrete) and noncohesive materials. The new power form (Eq. (12) made it possible to evaluate the initial modulus even for the case of unconfined condition (σc=0). For unconfined condition, the initial modulus is correlated with unconfined compressive strength (Eq. (19).
-
.gif)
-
Fitting constant
-
.gif)
-
Fitting constant
-
.gif)
-
Fitting constant
-
.gif)
-
Modified parameter 1 for initial tangent modulus [intercept at (σe+σc)/Pa=1.0]
-
.gif)
-
Modified parameter 2 for initial tangent modulus [slope of the log(Ei/Pa) vs. log(σc/Pa) plot]
-
ρ
-
Density of the rock material
-
σ
-
Vertical stress
-
σc
-
Confining pressure
-
σe
-
Equivalent confinement to compensate for the cohesion
-
σt
-
Tensile strength
-
νd
-
Dynamic Poisson's ratio
-
νs
-
Static Poisson's ratio
-
 h
h -
Horizontal strain
-
 v
v -
Vertical strain
-
a
-
Constant parameter
-
A
-
Fitting constant
-
b
-
Constant parameter
-
B
-
Fitting constant
-
c
-
Cohesion
-
C
-
Fitting constant
-
E
-
Modulus of elasticity
-
Ec
-
Modulus of elasticity for concrete
-
Ed
-
Dynamic elastic modulus
-
Ei
-
Initial tangent modulus
-
Es
-
Static elastic modulus
-
Esec
-
Secant modulus
-
Etan
-
Static tangent modulus
-
fc′
-
Unconfined compressive strength for concrete
-
K
-
Parameter 1 for initial tangent modulus (intercept at σc/Pa=1.0)
-
MYBP
-
Million years before present
-
n
-
Parameter 2 for initial tangent modulus [slope of the log(Ei/Pa) vs. log(σc/Pa) plot]
-
Pa
-
Atmospheric PRESSURE=101.325 kPa
-
qu
-
Unconfined compressive strength
-
R2
-
Coefficient
-
VP
-
P-wave velocity
-
VS
-
S-wave velocity
-
XRD
-
X-ray diffraction
-
φ
-
Angle of internal friction
-
θ
-
Angle of inclination of the failure plan
Acknowledgements
The author acknowledges the support of King Fahd University of Petroleum and Minerals in providing computing and laboratory facilities. He is also grateful to Mr. Khaqan Khan and Mr. Hasan Zakaria for their assistance.

.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)