HOMEWORK SOLUTION
HW #2
GEOTECHNICAL ENGINEERING I
(Question no. 3.1, 3.2, 3.5, 3.7, & 3.9 ..Al-Khafaji textbook)
![]()
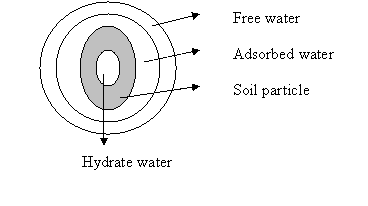
3.1 Explain the main differences between free water and hydration water as it relates to soil particles.
Answer:
Free water : Water which occupies the void of the soil which has primary influence on soil behavior, for granular soil it has no effect/influence on the individual particle structure when its removed but for clay is vice versa.
Hydration water : As a part of the crystal structure. Usually it cannot be removed by oven dry at 110o C except for gypsum & some tropical clay.
3.2 Determine the height of capillary rise above the free water table if the soil is silt with D10 = 0.055 mm. How long would it take for the water to achieve 50% of its maximum capillary rise and what would the corresponding pore water pressure be? Assume that k=10-6 cm/s.
Solution:
hc = 1.5/0.0055=272.73 cm
Z/hc =50%=0.5
See table 3.6 for uniform inorganic silt (assumed)
e max = 1.1
e min = 0.4
take the average e avg = (1.1+0.4)/2 = 0.75
h = e / (1+e) = 0.43
t = h . hc/K [ z/hc + ln (1 z/hc) ]
= (0.43 . 272.73/10-6) [ 0.5 + ln (1- 0.5) ]
= 22651123.14 second = 262.2 days
Pore water pressure
p = gw . h = 9.81 . (272.73/(2.100))
= 13.38 N/m2
3.5 A soil sample has a void ratio of 0.70 and a degree of saturation of 0.80. The specific gravity of solids is 2.70. Use SI units and assume gw = 9.81 kN/m3, then compute:
(a) Dry unit weight (gd )
(b) Bulk unit weight (gm)
(c) Saturated unit weight (gsat)
(d) Water content (w)
Solution:
(a) gd = Gs. gw/ (1+e)
= 2.7 x 9.81 / (1+0.7)
= 15.581 kN/m3
(b) gm = gd (1+w) where w = e. Sr/Gs = 0.7 . 0.8/ 2.7 = 0.207
= 15.581 (1+ 0.207)
= 18.81 kN/m3
(c)gsat = (Gs+e). gw /(1+e) = (2.7+0.7) . 9.81 / (1+0.7) = 19.62 kN/m3
(d) w= e. Sr/Gs = 0.7 . 0.8/ 2.7 = 0.207
3.7 A soil sample extracted from below the ground water table was determined to have a water content of 24% and a specific gravity of 2.75. Calculate the void ratio (e) and the saturated unit weight (gsat).
Solution:
e = w.Gs/Sr = 0.24 x 2.75 / 1 = 0.66
gsat = (Gs + e ) gw / (1+e) = (2.75+0.66) 9.81 / (1+0.66) = 20.15 kN/m3
or,
gsat = (Gs + e ) gw / (1+e) = (2.75+0.66) 62.4 / (1+0.66) = 128.18 pcf
3.9 For a saturated soil, given gd = 16 kN/m3 and w = 28%, determine:
(a)
Saturated unit weight (gsat)
(b) Void ratio (e)
(c) Specific gravity of the solid (Gs)
(d) Water content at 70% saturation (w at Sr=70%)
Solution:
(a) gsat = gd (1+w) = 16 (1+0.28) = 20.48 kN/m3
(b) e = (gsat
- gd
)/ (gd
- gb)
= (gsat
- gd
)/ (gd
(gsat-gw)
= (20.48 16)/(16 (20.48 9.81) = 4.48 / 5.33 = 0.84
(c) Gs = gd (1+e) / gw or, Gs = [gsat (1+0.84)/9.81] - 0.84 =3
= 16(1+0.84)/9.81
= 3
(d) w at Sr = 70%
w = Sr . e/Gs = 0.7 x 0.84 / 3 = 0.196 = 19.6%