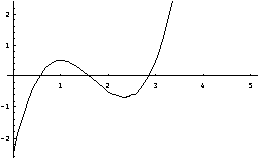CE317 Computer Methods in CE
Lecture
5*: Roots of Single Equations
We will discuss several methods for computing the roots of the single
equation f(x)=0, where f is generally nonlinear in x. Examples are polynomials,
rational functions, transcendental, etc. We will discuss the following methods:
1- Bracketing methods
a- The graphical method
b- The bisection method
c- The false-position method
2- Open methods
a- Fixed-Point Iteration method
b- Newton-Raphson method
c- The secant method
d- Modified Newton-Raphson method
Bracketing Methods
The Graphical Method:
It is the simplest root-finding method.
►Key-idea:
If we plot f(x) versus x, then the root or roots of f(x) are the values
of x at the intersections of f(x) with the x-axis.
►Procedure:
The function is first plotted using a wide range of x-axis so that we check the possibility of multiple roots and their locations. Then, the function is re-plotted several times where we narrow the range of x-axis in each next plot so that we can zoom into the area around each root. In this course we will use “Mathematica” for the repeated plotting due to its simplicity and efficiency.
►Examples:
Example1:
Estimate the root of the following equation
F(x)= x -Cos x
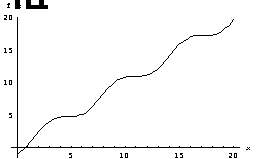
Solution: we first plot the above function with a big range of x, say [0,20], using the command:
![]()
The first figure shows that there is a single root and it is located in the range [0,2]. To get a better estimate we plot the function again using the range [0,2].
Range
of x-axis: [0,20] Range of x-axis: [0,2]
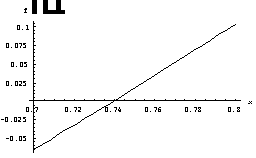
We repeat the process several times. The last refined figure suggests that the root is approximately 0.74 which is very close to the exact value of 0.7391. So that the true percent relative error is Єt=0.12%
Range
of x-axis: [0.5,1] Range of x-axis:
[0.7,0.8]
Example2:
Estimate the roots of the following equation
F(x)=
x3 –5 x2 +7x -2.5
Solution
Let us Plot it for the range 0<x<5. The plot shows that there are 3 roots.
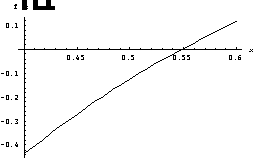
Root
1 is located within the range [0,1]
Root
2 is located within the range [1.5,2]
Root
3 is located within the range [2.75,3]
In
order to estimate each root we need to do the same procedure of the previous
example. For the first root, we get:
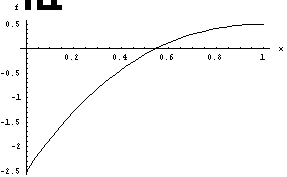

The
third plot suggests that the first root is x@0.55 (The exact value is 0.5484). If we repeat the procedure
for other roots, we get x@1.6 (The
exact value is 1.5970) and x@2.85 (the exact is 2.8546).
►Advantages
1- Does not require any formulation
2- Useful tool for understanding the behavior
of the function
3- Capable of estimating multiple roots
►Disadvantages
1-
Requires
repeated plotting
2-
Can not be
implemented in a computer program and therefore, not suited for problems
involving repeated finding of roots
The Bisection Method:
►Key-idea:
Assume that the function f(x) is continuous over an interval [xl,xu].
If the sign of f(x) changes over that interval (i.e. f(xl)=-f(xu)),
then we are sure that there is at least one root located within the interval.
►Procedure:
1-
Choose two
initial guesses for the lower value (xll) and the upper value (x1u) of the root . The choice must satisfy the inequality f(xl)*f (xu) < 0.
2-
Estimate the
first guess of the root by x1r = (x1l +x1u)/2.
3-
Calculate the
second guesses for the lower value (x2l)and the upper value (x2u) of the root by
if f (x1l )
*f(x1r) < 0, then: x2l = x1l and x2u = x1r
if f (x1l )
*f(x1r) > 0 then: x2l = x1r and x2u = x1u
4-
Estimate the
second guess of the root by x2r = (x2l +x2u)/2.
5-
Repeat step 3
and 4 until xir / x(i-1)r *100 < |εs|

Example1: Use the bisection method to find the root
of the equation
x
-cox(x) = 0 with a percent relative error
|εt|≤ 1%.
Solution
We have seen before that there is a single root lies in the interval [0,1]. Therefore, we start with xl=0. and xu=1., then iterate using the same procedure followed in example 1 to get the following tabulated results:
|
Iter |
Xl |
Xu |
Xr |
F(Xl) |
F(Xu) |
F(Xr) |
|εt| |
|
1 |
0. |
1. |
0.5 |
-1.0000 |
0.4597 |
-0.3776 |
32.35 |
|
2 |
0.5 |
1. |
0.75 |
-0.3776 |
0.4597 |
0.0183 |
1.48 |
|
3 |
0.5 |
0.75 |
0.625 |
-0.3776 |
0.0183 |
-0.1860 |
15.44 |
|
4 |
0.625 |
0.75 |
0.6875 |
-0.1860 |
0.0183 |
-0.0853 |
6.98 |
|
5 |
0.6875 |
0.75 |
0.7188 |
-0.0853 |
0.0183 |
-0.0339 |
2.75 |
|
6 |
0.7188 |
0.75 |
0.7344 |
-0.0339 |
0.0183 |
-0.0079 |
0.64 |
The method converges with the required accuracy after 5 iterations.
►Advantages
1- Simple concept and easy to program.
2- Convergence is guaranteed (provided that
f(x) is continuous ).
►Disadvantages
1- It requires a
previous knowledge of intervals that bracket the roots.