CE317 Computer Methods in CE

Lecture 4*: Taylor Series-Cont.

Use of Taylor series to approximate differential operators:

There are three ways to numerically approximate the first order derivative of a function:

1- 1^st order forward finite difference:

Consider the 1^st order Taylor series:

which yields: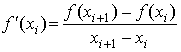

which can be written as

(1)

where h is called the interval or step size.

2- 1^st order backward finite difference:

If we write the 1^st order Taylor series backward, we get:

or:

(2)

3- 1^st order centered finite difference:

The formula can be obtained by subtracting (2) from (1) to get:

(3)

Example:

Use the forward, the backward and the centered difference approximations to estimate the first derivative of f(x)=e^2x+1 at x=2 using a step size h=0.2.

Approximation for the second order derivatives can be derived using the following procedure:

Recall the 2^nd order Taylor series:

which can be written as

or:

(4)

using (3) in (4), we can express f^’’_i in terms of f_i-1 , f_i and f_i+1:

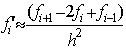
which is the second order centered finite difference. Similar procedure can be used to obtain the second order backward and forward finite differences.

Example:

Given the following data for the deflection y(x) of a beam of length L = 1m and EI = 1 N.m², estimate the numerical value for the bending moment at the middle of the beam.

x	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Y(x)	0.	-2.6	-4.9	-5.7	-7.9	-8.3	-7.7	-5.5	-4.8	-2.5	0.

---

* Important: This handout is only a summery of the lecture. The student take detailed notes during the class and refer to the textbook for more examples and discussion.