CE317 Computer Methods in CE
Lecture
3*:
Taylor series-Cont.
Example1:
Estimate
the polynomial f(x)=-0.1 x4 -0.15 x3 -0.5 x2 -0.25
x +1.2 at x=1 from its value and derivatives at x=0, using zero, 1st,
2nd, 3rd and 4th order Taylor series. Compare
the relative errors in the five approximations.
Solution:
WE need to obtain
the first 4 derivatives:
Also, we need to
compute f(0),f’(0),f’’(0), etc.:
Zero order Taylor
series:
1st
order Taylor series:
![]()
2nd
order Taylor series:
3nd
order Taylor series:
4th order Taylor
series:
Example2:
Repeat
Example 1 if f(1) is estimated from its value and derivatives at x=0.5.
Solution:
Zero order Taylor
series:
1st
order Taylor series:
2nd order
Taylor series:
3nd
order Taylor series:
4th order Taylor
series:
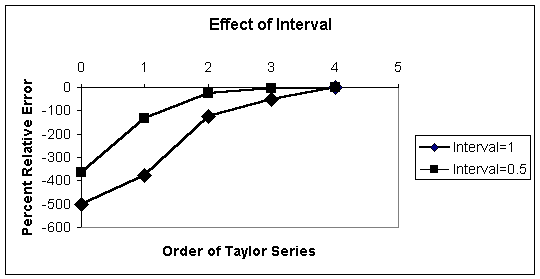
To
see the effect of the size of the interval, let us plot error versus order of
Taylor series for the two intervals of 1 and 0.5:
Example
3:
Use
Taylor series to estimate f(x)=Cos(x) at xi+1=π/3 with xi= π/4.
a-
Can we get a
0% error using Taylor series?
b-
Employ zero,
1st, 2nd, 3rd order expansions and compute the
relative errors in each case.
Solution:
Note:
Taylor series can
be generated by Mathematica using the built-in function ‘Series’ according to
the following format:
Series[function(x),
{x,x0,n}],
which generates a
power series in x using the values of the function and its n derivatives
evaluated at x0.