CE317 Computer Methods
in Civil Engineering
Lecture 2*: Computer Implementation
Steps of Computer
Implementation
1- Algorithm:
the sequence of logical steps required to perform a numerical procedure for
solving a certain problem
2-
Flow Chart: a
graphical representation of an algorithm. It consists of a series of blocks and
arrows. Each block represent a certain task or operation. The arrows represent
the sequence in which the operations are performed.
3-
Code: a
set of step-by-step commands that instructs the computer to carry out the
required calculations according to the designed algorithm or flow chart. The
code can be written in various computer languages such as Fortran, BASIC,
Visual BASIC, C, etc. There are also software “packages” that have more
powerful built-in functions to perform different types of numerical, symbolic
and graphical analyses such as MATLAB, Mathematica, Excel, etc.
To illustrates the above 3
steps, let consider the example of obtaining the roots of the quadratic equation
Ax2+Bx+C=0:
The algorithm and flow chart for this
problem can be written as:
Step 1: Begin the calculation.
Step 2: Input the values of the
coefficients
A, B and C
Step 3: Compute DISC=B2-4AC
Step 4: If DISC < 0, print:
”No REAL ROOTS”
Otherwise, compute:
ROOT1=(-B+DISC)/2A
ROOT2=(-B-DISC)/2A
Step 5: Print the values of the roots
The above flow chart can be
implemented in the following Fortran code:
If
Mathematica is used the above code reduces to a single command:
If a=1, b=4 and
c=1, we can evaluate the roots using
%/. :
If we want a
numerical value, we use the function N:
Approximation
& Errors
Mathematical
Definition of Errors:
If the true
solution is known, then the accuracy of the numerical solution can be measured
using the true percent relative error that can be defined as
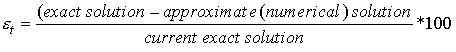
The exact solution is not known for many problems and therefore, the above formula becomes useless. Since the numerical solution is obtained using an iterative procedure, we can measure the accuracy of the numerical solution using
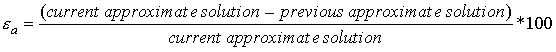
where εa is the approximate percent relative error.
Types of Errors:
1-
Round-off errors:
They are due to the computer imperfection
in dealing with numbers. For example: the quantities π, 71/2, e, etc. cannot be
represented exactly by the a limited number of digits provided by a certain
computer.
2-
Truncation errors:
They are due to approximating the exact formulation of the problem by an approximate (numerical) formulation. These errors are related to Taylor series as will be explained later.
3-
Blunders:
They are due to human errors and machine imperfections.
4-
Formulation
errors
5-
Errors due to
assumptions and data uncertainty
We will discuss the second type of errors in more details because they are associated with the process of approximation performed in most of the numerical methods considered in this course.
The Taylor Series
Taylor’s theorem:
Let the function f(x) and its n derivatives be continuous on an interval [xi
, xi+1], then the
function evaluated at xi+1 can be estimated from its value at xi
through the following series:
Zero order Taylor
series:
![]()
1st
order Taylor series:
![]()
2nd
order Taylor series:
![]()
nth order Taylor series:
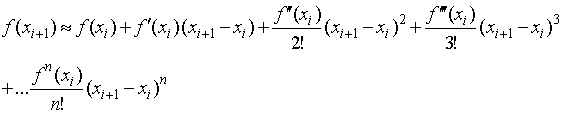
The accuracy of the above representation depends on the
following factors:
1-
Type of f(x):
The series is exact if nth order series is used to represent an nth
order polynomial. The case is not true if f(x) involves functions that do not
have vanishing (n+1)th derivatives. Examples are: Sin(x), ex,
Ln(x).
2-
The size of
the interval [xi , xi+1]: More accurate for shorter intervals.
3-
The number of
terms in the series: More accurate for more terms (not always true)
Use of Taylor series to
approximate functions
Example1:
Estimate the polynomial f(x)=-0.1 x4 -0.15 x3 -0.5 x2 -0.25 x +1.2 at x=1 from its value and derivatives at x=0, using zero, 1st, 2nd, 3rd and 4th order Taylor series. Compare the relative errors in the five approximations.